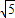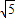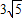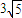题目内容
能够使得圆x2+y2-2x+4y+1=0上恰有两个点到直线2x+y+c=0距离等于1的c的一个值为( )
| A、2 | ||
B、
| ||
| C、3 | ||
D、3
|
分析:本题如果设圆上一点的坐标,用点到直线的距离公式得到一个方程,进而研究方程解的个数,将是非常麻烦的.所以可结合图形,圆心M到直线的距离大于1小于3时,圆M恰有两个点到直线的距离等于1,利用点到直线的距离公式列出关于c的不等式,求出解集,然后判断各选项即可.
解答:
解:圆的方程可化为:(x-1)2+(y+2)2=4,所以圆心M(1,-2),半径r=2,
结合图形容易知道,当且仅当M到直线l:2x+y+c=0的距离d∈(1,3)时,⊙M上恰有两个点到直线l的距离等于1,
由d=
∈(1,3)得:c∈(-3
,-
)∪(
,3
),而
<3<3
,所以满足题意的c可以是3.
故选C

解:圆的方程可化为:(x-1)2+(y+2)2=4,所以圆心M(1,-2),半径r=2,
结合图形容易知道,当且仅当M到直线l:2x+y+c=0的距离d∈(1,3)时,⊙M上恰有两个点到直线l的距离等于1,
由d=
| |c| | ||
|
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
故选C
点评:本题考查学生灵活运用点到直线的距离公式化简求值,会求不等式的正整数解.会利用数形结合的数学思想解决数学问题.是一道综合题.

练习册系列答案
相关题目