题目内容
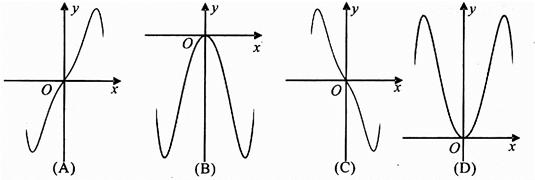
如图,函数y=f(x)的图象为折线ABC,设g(x)=f[f(x)],则函数y=g(x)的图象为( )
A. | B. | C. | D. |

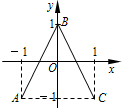
如图:函数y=f(x)的图象为折线ABC,函数f(x)为偶函数,
我们可以研究x≥0的情况即可,
若x≥0,可得B(0,1),C(1,-1),这直线BC的方程为:lBC:y=-2x+1,x∈[0,1],其中-1≤f(x)≤1;
若x<0,可得lAB:y=2x+1,∴f(x)=
,
我们讨论x≥0的情况:如果0≤x≤
,解得0≤f(x)≤1,此时g(x)=f[f(x)]=-2(-2x+1)=4x-1;
若
<x≤1,解得-1≤f(x)<0,此时g(x)=f[f(x)]=2(-2x+1)=-4x+3;
∴x∈[0,1]时,g(x)=
;
故选A;
我们可以研究x≥0的情况即可,
若x≥0,可得B(0,1),C(1,-1),这直线BC的方程为:lBC:y=-2x+1,x∈[0,1],其中-1≤f(x)≤1;
若x<0,可得lAB:y=2x+1,∴f(x)=
|
我们讨论x≥0的情况:如果0≤x≤
| 1 |
| 2 |
若
| 1 |
| 2 |
∴x∈[0,1]时,g(x)=
|
故选A;

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目

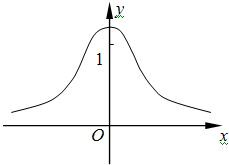
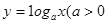 ,且
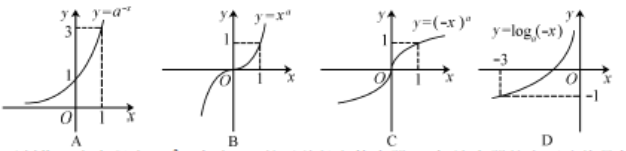
,且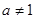 )的图像如右图所示,则下列函数图像正确的是
)的图像如右图所示,则下列函数图像正确的是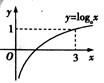
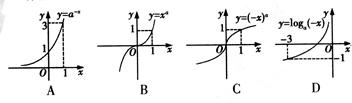
 的图象如右图所示,则下列函数正确的是 ( )
的图象如右图所示,则下列函数正确的是 ( )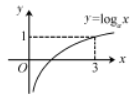
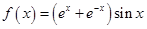 的部分图象大致为( )
的部分图象大致为( )