题目内容
已知曲线C是动点M到两个定点O(0,0)、A(3,0)距离之比为
的点的轨迹.
(1)求曲线C的方程;
(2)求过点N(1,3)与曲线C相切的直线方程.
| 1 |
| 2 |
(1)求曲线C的方程;
(2)求过点N(1,3)与曲线C相切的直线方程.
(1)设点M(x,y),则
|OM|=
,|AM|=
∵
=
,∴|AM|=2|OM|即
=2
…4分
两边平方整理,得:x2+y2+2x-3=0,即为所求曲线C的方程.…6分
(2)由(1)得x2+y2+2x-3=0,整理得(x+1)2+y2=4
∴曲线C是以(-1,0)为圆心,半径r=2的圆.
i)当过点N(1,3)的直线的斜率不存在时,直线方程为x=1,显然与圆相切;…8分
ii) 当过点N(1,3)的直线的斜率存在时,设方程为y-3=k(x-1)
即kx-y+3-k=0 …9分
∵直线与圆相切.得圆心到该直线的距离等于半径,
∴
=2,解之得k=
,…11分
可得直线方程为5x-12y+31=0 …12分
所以过点N(1,3)与曲线C相切的直线方程为x=1或5x-12y+31=0.…13分
|OM|=
| x2+y2 |
| (x-3)2+y2 |
∵
| |OM| |
| |AM| |
| 1 |
| 2 |
| (x-3)2+y2 |
| x2+y2 |
两边平方整理,得:x2+y2+2x-3=0,即为所求曲线C的方程.…6分
(2)由(1)得x2+y2+2x-3=0,整理得(x+1)2+y2=4
∴曲线C是以(-1,0)为圆心,半径r=2的圆.
i)当过点N(1,3)的直线的斜率不存在时,直线方程为x=1,显然与圆相切;…8分
ii) 当过点N(1,3)的直线的斜率存在时,设方程为y-3=k(x-1)
即kx-y+3-k=0 …9分
∵直线与圆相切.得圆心到该直线的距离等于半径,
∴
| |-k+0+3-k| | ||
|
| 5 |
| 12 |
可得直线方程为5x-12y+31=0 …12分
所以过点N(1,3)与曲线C相切的直线方程为x=1或5x-12y+31=0.…13分

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
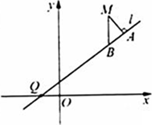
 和到直线y=
和到直线y= 距离相等的点的轨迹,l是过点Q(-1,0)的直线,M是C上(不在l上)的动点;A、B在l上,MA⊥l,MB⊥x轴(如图),
距离相等的点的轨迹,l是过点Q(-1,0)的直线,M是C上(不在l上)的动点;A、B在l上,MA⊥l,MB⊥x轴(如图), 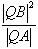 为常数。
为常数。
 的点的轨迹.
的点的轨迹.