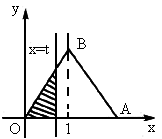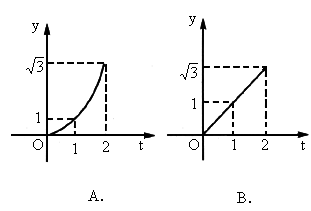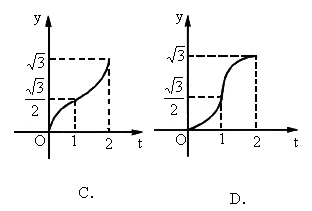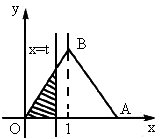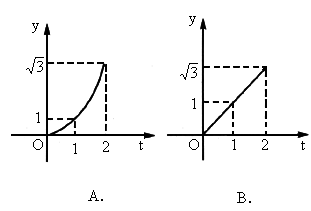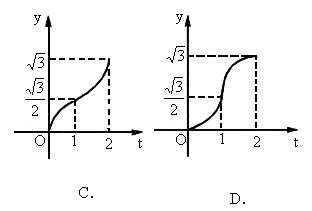题目内容
如图△OAB是边长为2的正三角形,这个三角形位于直线x=t左边的图形的面积为y,求函数y=f(t)的定义域、值域解析式,并作出其图形.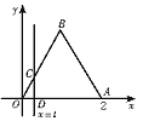
答案:
解析:
解析:
| ∵△ABC是正三角形,且边长为2,
∴图中各点坐标为A(2,0),B(1, ∵|DA|=2-t,同法yC= ∴当0≤t≤1时,y=f(t)= 当1<t≤2时,y=f(t)=S△OAB-S△CDA= - 再注意到,当t<0时,显然有y=0,当t>2时,有y= ∴y=f(t)= 此函数的定义域为R,值域为[0,
|

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
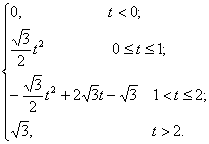
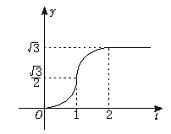
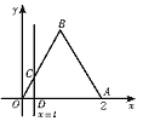
 如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式.
如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式.