题目内容
△ABC的BC边上的高线为AD，BD=a，CD=b，且a＜b，将△ABC沿AD折成大小为θ的二面角B-AD-C，若cosθ=
，则此时△ABC是（ ）
| a |
| b |
分析：根据折叠前AD与BD、CD的垂直性，可证∠BDC为二面角的平面角，再利用余弦定理求出a、b、c之间的关系，从而判断三角形的形状．
解答：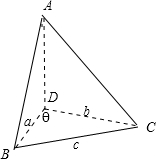
解：∵AD是△ABC，BC边上的高，∴AD⊥BD，AD⊥CD，
∴∠BDC为二面角B-AD-C的平面角，∠BDC=θ
设BC=c，则c2=a2+b2-2abcosθ=a2+b2-2ab×
=b2-a2，即b2=a2+c2，
AB=
；AC=
，
∴c2=BC2=AC2-AB2，
∴折叠后△ABC为直角三角形．
故选C．
解：∵AD是△ABC，BC边上的高，∴AD⊥BD，AD⊥CD，∴∠BDC为二面角B-AD-C的平面角，∠BDC=θ
设BC=c，则c2=a2+b2-2abcosθ=a2+b2-2ab×
| a |
| b |
AB=
| a2+AD2 |
| b2+AD2 |
∴c2=BC2=AC2-AB2，
∴折叠后△ABC为直角三角形．
故选C．
点评：本题借助折叠图形，考查了二面角平面角的定义，余弦定理；利用余弦定理导出三角形的边长之间的关系是解答本题的关键．
练习册系列答案
相关题目
已知AM是△ABC的BC边上的中线，若
=
、
=
，则
等于（ ）
| AB |
| a |
| AC |
| b |
| AM |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
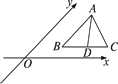
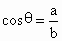，则三棱锥A－BDC的侧面△ABC是