题目内容
已知函数y=f（x）是R上的偶函数，且在区间（-∞，0）是单调递增的，若S1=
x2dx，S2=
dx，S3=
exdx则下列不等式中一定成立的是（ ）
| ∫ | 21 |
| ∫ | 21 |
| 1 |
| x |
| ∫ | 21 |
| A．f（S1）＜f（S2）＜f（S3） | B．f（S3）＜f（S2）＜f（S1） |
| C．f（S2）＜f（S1）＜f（S3） | D．f（S3）＜f（S1）＜f（S2） |
根据积分公式可知S1=
x3
=
-
=
，S2=lnx
=ln2，S3=ex
=e2-e，
∵函数y=f（x）是R上的偶函数，且在区间（-∞，0）是单调递增，
∴在区间（0，+∞）是单调递减，
∵e2-e＞
＞ln2＞0，
∴f（S3）＜f（S1）＜f（S2），
故选：D．
| 1 |
| 3 |
| | | 21 |
| 8 |
| 3 |
| 1 |
| 3 |
| 7 |
| 3 |
| | | 21 |
| | | 21 |
∵函数y=f（x）是R上的偶函数，且在区间（-∞，0）是单调递增，
∴在区间（0，+∞）是单调递减，
∵e2-e＞
| 7 |
| 3 |
∴f（S3）＜f（S1）＜f（S2），
故选：D．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
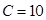，面积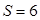
，求这个扇形的半径
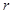和圆心角
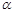的弧度数.
