题目内容
若规定E={a1，a2…a10}的子集{ak1，ak2…akn}（1≤n≤10）为E的k级子集，其中k=2k1-1+2k2-1+…+2kn-1，那么集合{a1，a2，a5，a7，a8}将是E的M级子集，则M为（ ）
分析：根据题意，由E的k级子集的定义，若集合{a1，a2，a5，a7，a8}将是E的M级子集，则M=2°+21+24+26+27=1+2+16+64+128，计算可得答案．
解答：解：根据题意，对于集合{a1，a2，a5，a7，a8}将是E的M级子集，
则M=2°+21+24+26+27=1+2+16+64+128=211；
故选D．
则M=2°+21+24+26+27=1+2+16+64+128=211；
故选D．
点评：本题是新定义的题型，关键是正确理解题意中E的k级子集的定义以及k的计算方法．
练习册系列答案
相关题目
为集合E＝{a1，a2，…，a10}的第k个子集，其中
，若
，则k1＋k2＋…＋km的值是
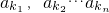（1≤n≤10）为E的k级子集，其中k=
+
+…+
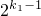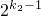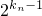，那么集合{a1，a2，a5，a7，a8}将是E的M级子集，则M为
（1≤n≤10）为E的k级子集，其中k=
+
+…+
，那么集合{a1，a2，a5，a7，a8}将是E的M级子集，则M为（ ）