题目内容
已知y＝f(x)是定义在R上的奇函数，当x≤0时，f(x)＝2x＋x2.
（1）求x>0时，f(x)的解析式；
（2）若关于x的方程f(x)＝2a2＋a有三个不同的解，求a的取值范围．
【答案】
（1）x>0时，f(x)＝2x－x2.
（2）－1<a<
.
【解析】
试题分析：(1)任取x>0，则－x<0，
∴f(－x)＝－2x＋(－x)2＝x2－2x.
∵f(x)是奇函数，
∴f(x)＝－f(－x)＝2x－x2.
故x>0时，f(x)＝2x－x2.
(2)∵方程f(x)＝2a2＋a有三个不同的解，
∴－1<2a2＋a<1.∴－1<a<.
考点：奇函数，以及函数与方程
点评：主要是考查了函数的奇偶性以及函数与方程的问题的运用，属于中档题。
练习册系列答案
阅读快车系列答案
相关题目
＋2at)x＋3at＋b＝0，直线l的
，则当t为何值时，f(t)有最大值，最大值是多少？
)在曲线C上，又在直线l上，求
的取值范围．
＜0的解集是________．
(x∈R)，P1(x1，y1)、P2(x2，y2)是函数y＝f(x)图象上两点，且线段P1P2中点P的横坐标是
．
)(m∈N*，n＝1，2，…m)，求数列{an}的前m项和Sm；
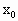恒成立，求实数a的取值范围．
是x＝x0为极值点的既不充分也不必要条件；
, 则
(其中
)；