题目内容
以下命题:
①若|
•
|=|
|•|
|,则
∥
;
②
=(-1,1)在
=(3,4)方向上的投影为
;
③若△ABC中,a=5,b=8,c=7,则
•
=20;
④若非零向量
、
满足|
+
|=|
|,则|2
|>|
+2
|.
⑤已知△ABC中,
=
(
+
+
)则向量λ(
+
)(λ≠0)所在直线必过N点.其中所有真命题的序号是
①若|
| a |
| b |
| a |
| b |
| a |
| b |
②
| a |
| b |
| 1 |
| 5 |
③若△ABC中,a=5,b=8,c=7,则
| BC |
| CA |
④若非零向量
| a |
| b |
| a |
| b |
| b |
| b |
| a |
| b |
⑤已知△ABC中,
| PN |
| 1 |
| 3 |
| PA |
| PB |
| PC |
| AB |
| AC |
①②④
①②④
.分析:①由|
•
|=|
|•|
|,知cos<
,
>=±1,由此能判断①的正误;
②
=(-1,1)在
=(3,4)方向上的投影为|
|•cos<
,
>,由此能判断②的正误;
③若△ABC中,由a=5,b=8,c=7,知cos∠ACB=
,由
•
=|
|•|
|•(-cos∠ACB)能求出结果;
④由|
+2
|=|
+
+
|≤|
+
|+|
|=2|
|,能推导出|2
|>|
+2
|;
⑤△ABC中,设A(0,1),B(2,4)C(6,1),P(x,y),利用特值法能得到向量λ(
+
)(λ≠0)所在直线不一定过N点.
| a |
| b |
| a |
| b |
| a |
| b |
②
| a |
| b |
| a |
| a |
| b |
③若△ABC中,由a=5,b=8,c=7,知cos∠ACB=
| 1 |
| 2 |
| BC |
| CA |
| BC |
| CA |
④由|
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| b |
| b |
| b |
| a |
| b |
⑤△ABC中,设A(0,1),B(2,4)C(6,1),P(x,y),利用特值法能得到向量λ(
| AB |
| AC |
解答:解:①若|
•
|=|
|•|
|,则cos<
,
>=±1,
∴
∥
,故①正确;
②
=(-1,1)在
=(3,4)方向上的投影为|
|•cos<
,
>=
×
=
,故②正确;
③若△ABC中,∵a=5,b=8,c=7,
∴cos∠ACB=
=
,
∴
•
=|
|•|
|•(-cos∠ACB)=5×8×(-
)=-20,故③不正确;
④∵|
+2
|=|
+
+
|≤|
+
|+|
|=2|
|,
∵
,
是非零向量,
∴必有
+
≠
,
∴上式中等号不成立.
∴|2
|>|
+2
|,故④正确;
⑤△ABC中,设A(0,1),B(2,4)C(6,1),P(x,y),
λ(
+
)=λ[(2,3)+(6,0)]=λ(8,3)=(8λ,3λ),
∵
=
(
+
+
),
∴(x2-x,y2-y )=
(8-3x,6-3y)=(
-x,2-y),
∴N(
,2).
∴向量λ(
+
)(λ≠0)所在直线不一定过N点,故⑤不正确.
故答案为:①②④.
| a |
| b |
| a |
| b |
| a |
| b |
∴
| a |
| b |
②
| a |
| b |
| a |
| a |
| b |
| 2 |
| -3+4 | ||
|
| 1 |
| 5 |
③若△ABC中,∵a=5,b=8,c=7,
∴cos∠ACB=
| 64+25-49 |
| 2×5×8 |
| 1 |
| 2 |
∴
| BC |
| CA |
| BC |
| CA |
| 1 |
| 2 |
④∵|
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| b |
| b |
∵
| a |
| b |
∴必有
| a |
| b |
| b |
∴上式中等号不成立.
∴|2
| b |
| a |
| b |
⑤△ABC中,设A(0,1),B(2,4)C(6,1),P(x,y),
λ(
| AB |
| AC |
∵
| PN |
| 1 |
| 3 |
| PA |
| PB |
| PC |
∴(x2-x,y2-y )=
| 1 |
| 3 |
| 8 |
| 3 |
∴N(
| 8 |
| 3 |
∴向量λ(
| AB |
| AC |
故答案为:①②④.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,注意平面向量知识的合理运用.

练习册系列答案
相关题目
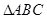 中,若
中,若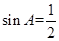 ,则
,则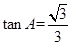 ;
;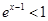 ”是“
”是“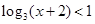 ”的必要不充分条件;
”的必要不充分条件;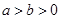 且
且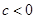 ,则
,则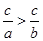 ”的逆命题是真命题.
”的逆命题是真命题.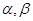 是两个不同的平面,
是两个不同的平面,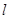 是一条直线,以下命题正确的是
是一条直线,以下命题正确的是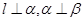 ,则
,则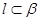 B.若
B.若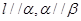 ,则
,则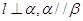 ,则
,则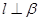 D.若
D.若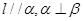 ,则
,则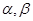 是两个不同的平面,
是两个不同的平面,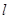 是一条直线,以下命题正确的是
是一条直线,以下命题正确的是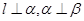 ,则
,则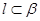 B.若
B.若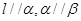 ,则
,则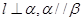 ,则
,则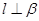 D.若
D.若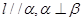 ,则
,则