题目内容
请阅读下列命题:① 直线y=kx+1与椭圆![]() 总有两个交点;
总有两个交点;
② f(x)=2sin(3x-![]() )的图像可由f(x)=2sin3x按向量a=(-
)的图像可由f(x)=2sin3x按向量a=(-![]() ,0)平移得到;
,0)平移得到;
③ 在R上连续的函数f(x)若是增函数,则对于任意x0∈ R,均有![]() (x0)>0成立;
(x0)>0成立;
④ 抛物线x=ay2(a≠0)的焦点坐标是(![]() ,0);
,0);
以上4个命题中,真命题是____________(写出所有真命题的编号).
①④
解析:本题考查了直线与椭圆的位置关系、抛物线的方程与性质、函数的图像与平移及函数连续与极限等知识.①中直线y=kx+1恒过定点P(0,1),点P在椭圆内部,所以直线与椭圆总有两个交点;②f(x)=2sin3x按向量a=(-![]() ,0)平移得到f(x)=2sin(3x+
,0)平移得到f(x)=2sin(3x+![]() );③举例f(x)=x3在R上连续且为增函数,但f(0)=0.④抛物线方程y2=
);③举例f(x)=x3在R上连续且为增函数,但f(0)=0.④抛物线方程y2=![]() x,焦点位于x轴上,为(
x,焦点位于x轴上,为(![]() ,0).所以真命题是①④.
,0).所以真命题是①④.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
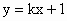 与椭圆
与椭圆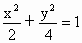 总有两个交点;
B.
总有两个交点;
B. 的图象可由f(x)=2sin3x按向量
的图象可由f(x)=2sin3x按向量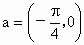 平移得到;
平移得到;
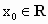 ,均有,
,均有,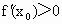 成立;
成立;
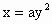 (a≠0)的焦点坐标是(
(a≠0)的焦点坐标是(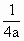 ,0).
,0).
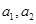 满足
满足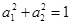 ,那么
,那么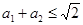 。”
。” ,因为对一切实数
,因为对一切实数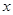 ,恒有
,恒有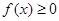 ,又
,又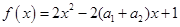 ,从而得
,从而得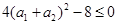 ,所以
,所以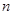 个正实数满足
个正实数满足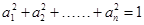 时,你可以构造函数
时,你可以构造函数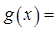 ,进一步能得到的结论为
。(不必证明)
,进一步能得到的结论为
。(不必证明)