Question

若函数y=f（x）（x∈R）满足f（x+2 ）=f（x），且x∈[-1，1]时，f（x）=|x|，函数y=g（x）是偶函数，且x∈（0，+∞）时，g（x）=|log3x|．则函数y=f（x）图象与函y=g（x）图象的交点个数为   

Answer 1

【答案】分析：结合函数的性质分别画出f（x），g（x）的简图，由图象观察交点个数．
解答：解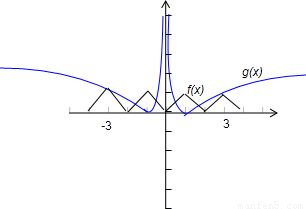：∵函数y=f（x）（x∈R）满足f（x+2 ）=f（x），
∴它是周期函数，周期是2，
∵函数y=g（x）是偶函数
∴它的图象关于y轴对称．
画图：
由图知，共6个交点．
故填：6．
点评：数形结合法是常用的解题方法，先根据题意画出函数的图象，再结合图象解答问题．交点个数的问题常用此法．