题目内容
阅读不等式2x+1＞3x的解法：
设f(x)=(
)x+(
)x，函数y=(
)x和y=(
)x在R内都单调递减；则f（x）在（-∞，+∞）内单调递减．
∵f（1）=1，∴当x＜1时，(
)x+(
)x＞1，当x≥1时，(
)x+(
)x≤1．
∵3x＞0，∴不等式2^+1＞3x的解为x＜1；
（1）试利用上面的方法解不等式2x+3x≥5x；
（2）证明：3x+4x=5x有且仅有一个实数解x=2．
设f(x)=(
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
∵f（1）=1，∴当x＜1时，(
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
∵3x＞0，∴不等式2^+1＞3x的解为x＜1；
（1）试利用上面的方法解不等式2x+3x≥5x；
（2）证明：3x+4x=5x有且仅有一个实数解x=2．
（1）设g(x)=(
)x+(
)x，函数y=(
)x和y=(
)x在R内都单调递减；则g（x）在（-∞，+∞）内单调递减，
∵g（1）=1，当x≤1时，(
)x+(
)x≥1，当x＞1时，(
)x+(
)x＜1；
∴不等式2x+3x≥5x的解集为：{x|x≤1}；
（2）令h(x)=(
)x+(
)x，函数y=(
)x和y=(
)x在R内都单调递减；则h（x在（-∞，+∞）内单调递减，
∵h（2）=2，当x＜2时，(
)x+(
)x＞1，当x＞2时，(
)x+(
)x＜1；
∴有且只有一个实数x=2使得(
)x+(
)x=1，即3x+4x=5x有且仅有一个实数解x=2．
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
∵g（1）=1，当x≤1时，(
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
∴不等式2x+3x≥5x的解集为：{x|x≤1}；
（2）令h(x)=(
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
∵h（2）=2，当x＜2时，(
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
∴有且只有一个实数x=2使得(
| 3 |
| 5 |
| 4 |
| 5 |
练习册系列答案
相关题目
，函数
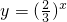和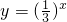
在R内都单调递减；则f（x）在（-∞，+∞）内单调递减．
．
；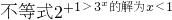