题目内容
已知定义在R上的函数f(x) 满足条件:(1)f(x)+f(-x)=2;(2)对非零实数x,都有2f(x)+f( )=2x+
)=2x+ +3.
+3.(1)求函数f(x)的解析式;
(2)设函数g(x)=
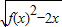 (x≥0)直线 y=
(x≥0)直线 y= n-x分别与函数f(x) 的反函数 交于A,B两点
n-x分别与函数f(x) 的反函数 交于A,B两点(其中n∈N*),设 an=|AnBn|,sn为数列an 的前n项和.求证:当n≥2 时,总有 Sn2>2(
 )成立.
)成立.
【答案】分析:(1)令解析式中的x用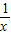 代入,得到一个方程组,消去f(
代入,得到一个方程组,消去f(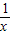 )可求出函数的解析式;
)可求出函数的解析式;
(2)先求出An的坐标,依题意得Bn与An关于y=x对称求出Bn的坐标,求出an,从而求出Sn,将sn2-sn-12进行累加可求证得结论.
解答:解:(1)由②知x≠0时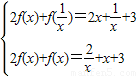 ⇒
⇒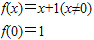
⇒f(x)=x+1(4分)
(2)g(x)=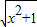 由
由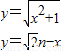 ⇒An(
⇒An( ,
,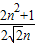 )
)
依题意得Bn与An关于y=x对称⇒Bn(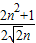 ,
,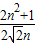 )=
)=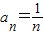 (6分)
(6分)
⇒sn=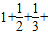 +
+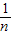 ⇒sn-sn-1=
⇒sn-sn-1=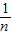 =
=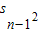 =sn2-
=sn2-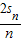 +
+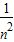 (8分)
(8分)
⇒sn2-sn-12=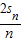
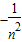 (n≥2)累加得sn2-s12=2(
(n≥2)累加得sn2-s12=2(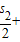
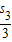 ++
++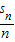 )-(
)-(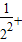
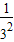 ++
++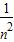 )
)
⇒sn2=2(
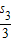 ++
++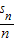 )+1-(
)+1-(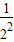
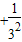 ++
++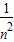 )(10分)
)(10分)
又1-(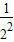
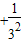 ++
++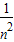 )>1-(
)>1-(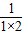
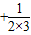 ++
++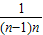 )=
)=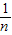 >0
>0
∴sn2>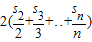 (12分)
(12分)
点评:本题主要考查了函数解析式的求解,以及数列的通项公式和求和,同时考查了利用累加法证明不等式,属于难题.
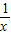 代入,得到一个方程组,消去f(
代入,得到一个方程组,消去f(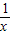 )可求出函数的解析式;
)可求出函数的解析式;(2)先求出An的坐标,依题意得Bn与An关于y=x对称求出Bn的坐标,求出an,从而求出Sn,将sn2-sn-12进行累加可求证得结论.
解答:解:(1)由②知x≠0时
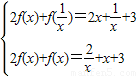 ⇒
⇒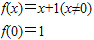
⇒f(x)=x+1(4分)
(2)g(x)=
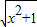 由
由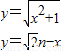 ⇒An(
⇒An( ,
,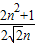 )
)依题意得Bn与An关于y=x对称⇒Bn(
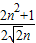 ,
,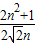 )=
)=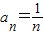 (6分)
(6分)⇒sn=
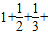 +
+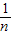 ⇒sn-sn-1=
⇒sn-sn-1=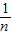 =
=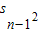 =sn2-
=sn2-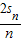 +
+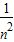 (8分)
(8分)⇒sn2-sn-12=
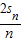
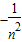 (n≥2)累加得sn2-s12=2(
(n≥2)累加得sn2-s12=2(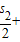
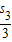 ++
++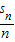 )-(
)-(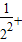
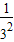 ++
++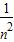 )
)⇒sn2=2(

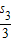 ++
++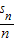 )+1-(
)+1-(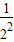
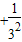 ++
++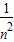 )(10分)
)(10分)又1-(
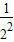
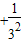 ++
++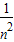 )>1-(
)>1-(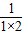
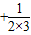 ++
++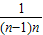 )=
)=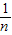 >0
>0∴sn2>
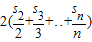 (12分)
(12分)点评:本题主要考查了函数解析式的求解,以及数列的通项公式和求和,同时考查了利用累加法证明不等式,属于难题.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |