题目内容
已知函数
(I)若不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(II)在(I)的条件下,若 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
(Ⅰ)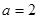 ;(Ⅱ)
;(Ⅱ)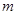 的取值范围为(-∞,5].
的取值范围为(-∞,5].
【解析】
试题分析:(Ⅰ)不等式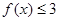 的解集为
的解集为 ,求实数a的值,首先解不等式
,求实数a的值,首先解不等式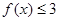 ,解得
,解得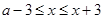 ,利用解集为
,利用解集为 ,从而求出
,从而求出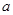 的值;(Ⅱ)若
的值;(Ⅱ)若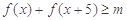 对一切实数
对一切实数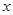 恒成立,转化为求
恒成立,转化为求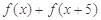 的最小值,只要实数
的最小值,只要实数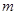 的取值小于或等于它的最小值,不等式
的取值小于或等于它的最小值,不等式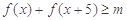 对一切实数
对一切实数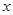 恒成立,故关键点是求
恒成立,故关键点是求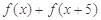 的最小值,由(Ⅰ)知
的最小值,由(Ⅰ)知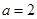 ,故
,故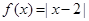 ,设
,设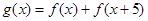 ,于是
,于是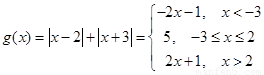 ,易求出最小值为5,则
,易求出最小值为5,则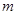 的取值范围为(-∞,5].
的取值范围为(-∞,5].
试题解析:(Ⅰ)由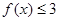 得
得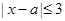 ,解得
,解得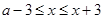 .又已知不等式
.又已知不等式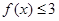 的解集为
的解集为 ,所以
,所以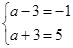 ,解得
,解得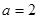 .
.
(Ⅱ)当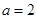 时,
时,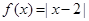 ,设
,设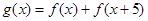 ,于是
,于是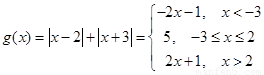 ,所以当
,所以当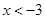 时,
时,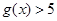 ; 当
; 当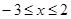 时,
时,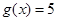 ;当
;当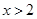 时,
时,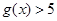 .综上可得,
.综上可得, 的最小值为5.从而若
的最小值为5.从而若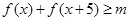 ,即
,即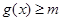 对一切实数
对一切实数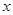 恒成立,则
恒成立,则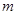 的取值范围为(-∞,5].
的取值范围为(-∞,5].
考点:本题考不等式的解法,考查学生数形结合的能力以及化归与转化思想.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
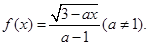
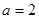 ,求
,求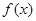 的定义域;
的定义域;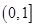 上是减函数,求实数
上是减函数,求实数 的取值范围.
的取值范围.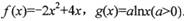
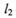 与函数
与函数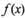 的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
的图象切于点R,求证 P,R,Q三点的横坐标成等差数列; 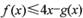 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;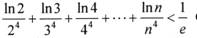 〔其中
〔其中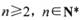 , e为自然对数的底数)
, e为自然对数的底数) 函数
函数 .
. 且函数
且函数 为奇函数,求实数
为奇函数,求实数 ;
; 试判断函数
试判断函数 ,
, ,
, 时,求函数
时,求函数 的对称轴或对称中心.
的对称轴或对称中心.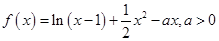 .
.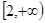 的最小值为f(t),求t的值。
的最小值为f(t),求t的值。