Question

设M是非空集合，且M⊆R，定义在R上的函数f_M（x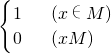）=的值域为

1. A.
   {0，1}
2. B.
   {0}
3. C.
   {1}
4. D.
   以上都不对

Answer 1

D
分析：根据定义思考，了解函数f_M（x）是怎样定义的；也就说这个函数是对集合R进行运算，集合R里是X这个元素，函数的值是1 否则是0．
解答：∵M是非空集合，且M⊆R，∴当M?R时，在R中，每个元素X有两种情况：X∈M，或X∉M；当X∈M时，f_M（x）=1，当X∉M时，f_M（x）=0；
当M=R时，R中每个元素X只有一种情况，X∈M，且f_M（x）=1；
所以，函数f_M（x）的值域为：{0，1}或{1}．
故选：D．
点评：本题用定义来考查函数的值域，答题时容易忽略M⊆R中的M=R这种情况，容易选择答案A．