题目内容
已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.
思路分析:本题主要考查三角函数的基础知识、余弦定理以及三角形的面积公式等.四边形为圆内接四边形,故四边形的对角互补,从而可知sinA=sinC,再结合四边形的四边已知,易求出四边形的两条对角线,从而求出其面积.
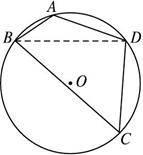
解:如图所示,连结BD,设四边形ABCD的面积为S,则
S=S△ABD+S△CBD
=![]() AB·AD·sinA+
AB·AD·sinA+![]() BC·CD·sinC.
BC·CD·sinC.
又sinA=sinC(∵A、C互补),
∴S=![]() (2×4+6×4)sinA=16sinA.
(2×4+6×4)sinA=16sinA.
又∵BD2=AB2+AD2-2AB·AD·cosA
=BC2+CD2-2BC·CD·cosC,
且cosA=-cosC(∵A、C互补),
∴64cosA=-32,即cosA=-![]() .
.
又∵0°<A<180°,
∴A=120°,即sinA=![]() ,
,
∴S=16sinA=8![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
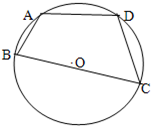 如图,已知圆内接四边形ABCD的边长分别为AB=2,BC=6,AD=CD=4.
如图,已知圆内接四边形ABCD的边长分别为AB=2,BC=6,AD=CD=4. 如图,已知圆内接四边形ABCD的边长为AB=2,BC=6,CD=DA=4,则四边形ABCD面积为( )
如图,已知圆内接四边形ABCD的边长为AB=2,BC=6,CD=DA=4,则四边形ABCD面积为( ) 如图已知圆内接四边形ABCD中,AB=2,BC=6,AD=CD=4,则四边形ABCD的面积S=
如图已知圆内接四边形ABCD中,AB=2,BC=6,AD=CD=4,则四边形ABCD的面积S=