题目内容
设a∈{-2,-
,-
,-
,
,1,2,3},已知幂函数y=xa为偶函数,且在(0,+∞)上递减,则a的所有可能取值为
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
-2,-
| 2 |
| 3 |
-2,-
.| 2 |
| 3 |
分析:先判断偶函数的幂函数,然后判断函数在(0,+∞)上递减的幂函数即可.
解答:解:a∈{-2,-
,-
,-
,
,1,2,3},
幂函数y=xa为偶函数,所以a∈{-2,-
,2},即y=x-2,y=x2,y=x-
,
在(0,+∞)上递减,有y=x-2,y=x-
,
所以a的可能值为:-2,-
.
故答案为:-2,-
.
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
幂函数y=xa为偶函数,所以a∈{-2,-
| 2 |
| 3 |
| 2 |
| 3 |
在(0,+∞)上递减,有y=x-2,y=x-
| 2 |
| 3 |
所以a的可能值为:-2,-
| 2 |
| 3 |
故答案为:-2,-
| 2 |
| 3 |
点评:本题考查幂函数的基本性质,函数必须满足两个条件,是解题的关键.

练习册系列答案
相关题目
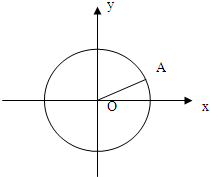 如图,设
如图,设