题目内容
从装有4粒大小、形状相同,颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),则倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率( )A.小
B.大
C.相等
D.大小不能确定
【答案】分析:根据题意,从4个不同的球中取出球的数目可以为1、2、3、4,进而可得总取法数目,又可得取到奇数个小球的取法与取到偶数个小球的取法数目,由古典概型的公式,计算可得答案.
解答:解:根据题意,从4个不同的球中取出球的数目为1、2、3、4,
其总取法为C41+C42+C43+C44=15种.
取到奇数个小球的取法有C41+C43=8种,
取到偶数个小球的取法有C42+C44=7种.
故倒出奇数粒玻璃球的概率为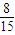 ,倒出偶数粒玻璃球的概率为
,倒出偶数粒玻璃球的概率为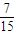 ,
,
所以倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率大,
故选B.
点评:本题考查组合、排列的应用以及古典概型的计算,注意分类讨论的运用.
解答:解:根据题意,从4个不同的球中取出球的数目为1、2、3、4,
其总取法为C41+C42+C43+C44=15种.
取到奇数个小球的取法有C41+C43=8种,
取到偶数个小球的取法有C42+C44=7种.
故倒出奇数粒玻璃球的概率为
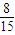 ,倒出偶数粒玻璃球的概率为
,倒出偶数粒玻璃球的概率为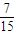 ,
,所以倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率大,
故选B.
点评:本题考查组合、排列的应用以及古典概型的计算,注意分类讨论的运用.

练习册系列答案
相关题目
从装有4粒大小、形状相同,颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),则倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率( )
| A、小 | B、大 | C、相等 | D、大小不能确定 |