题目内容
设椭圆C：
+
=1（a＞b＞0）的左，右焦点分别为F1，F2，离心率为e=
，以F1为圆心，|F1F2|为半径的圆与直线x-
y-3=0相切．
（I）求椭圆C的方程；
（II）过点S（0，-
）且斜率为k的直线交椭圆C于点A，B，证明无论k取何值，以AB为直径的圆恒过定点D（0，1）．
解：（I）设F1（-c，0），F2（c，0），则由已知得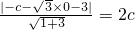
，
解得c=1．
∵
，∴
，∴b2=1，
∴椭圆C的方程为
．
（II）由已知直线AB：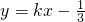
，代入，得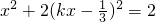
，
整理，得（18k2+9）x2-12kx-16=0，
设A（x1，y1），B（x2，y2），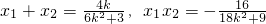
，
∵
，
∴
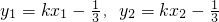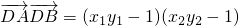
=（1+k2）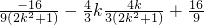
=0，∴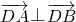
．∴以AB为直径的圆恒过定点D（0，1）．
分析：（I）设F1（-c，0），F2（c，0），则由已知得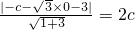，得c=1．再由能导出椭圆C的方程．
（II）由已知直线AB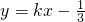：，代入，得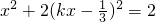，整理，得（18k2+9）x2-12kx-16=0，再由韦达定理进行求解．
点评：本题考查直线和圆锥曲线的位置关系，解题时要认真审题，仔细解答，注意公式的合理选用．
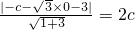，解得c=1．
∵
，∴，∴b2=1，∴椭圆C的方程为
．（II）由已知直线AB：
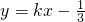，代入，得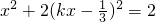，整理，得（18k2+9）x2-12kx-16=0，
设A（x1，y1），B（x2，y2），
，∵
，∴
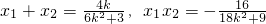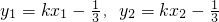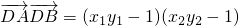
=（1+k2）
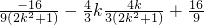=0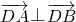，∴．∴以AB为直径的圆恒过定点D（0，1）．分析：（I）设F1（-c，0），F2（c，0），则由已知得
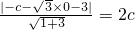，得c=1．再由能导出椭圆C的方程．（II）由已知直线AB：
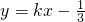，代入，得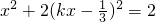，整理，得（18k2+9）x2-12kx-16=0，再由韦达定理进行求解．点评：本题考查直线和圆锥曲线的位置关系，解题时要认真审题，仔细解答，注意公式的合理选用．
练习册系列答案
相关题目
，
=1（a＞b＞0）的左、右焦点分别为F1、F2，离心率为
，左焦点F1到直线l：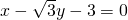
的距离等于长半轴长．
+
=1（a＞b＞0）过点M（1，1），离心率e=
，O为坐标原点．
•
为定值．
设椭圆C：
+
=1（a＞b＞0）的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q，且
=
．
y+3=0相切，求椭圆C的方程．
+
=1（a＞b＞0）的左焦点为F1=（-
，0），椭圆过点P（-
，
）