题目内容
设函数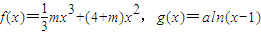 ,其中a≠0.
,其中a≠0.( I )若函数y=g(x)图象恒过定点P,且点P关于直线
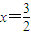 的对称点在y=f(x)的图象上,求m的值;
的对称点在y=f(x)的图象上,求m的值;(Ⅱ)当a=8时,设F(x)=f′(x)+g(x+1),讨论F(x)的单调性;
(Ⅲ)在(I)的条件下,设
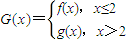 ,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
【答案】分析:(I)先得出点P关于直线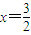 的对称点(1,0),由题意可得f(1)=0,求出m的值;
的对称点(1,0),由题意可得f(1)=0,求出m的值;
(II)先求函数定义域,然后对函数求导,再对字母m分类讨论:当m≥0时,当m<0时.分别解f′(x)>0,f′(x)<0,求解即可.
(III)对于存在性问题,可先假设存在,即假设曲线y=G(x)上存在两点P、Q,满足题意,则P、Q只能在y轴的同侧,再利用△OPQ是以O为直角顶点的直角三角形,求出a的取值范围,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(I)令ln(x-1)=0,得x=2,∴点P关于直线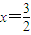 的对称点(1,0),
的对称点(1,0),
∴f(1)=0, m+4+m=0,m=-3.
m+4+m=0,m=-3.
(II)F(x)=f′(x)+g(x+1)mx2+2(4+m)x+8lnx,(x>0).
∴F′(x)=2mx+(8+2m)x+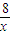 =
=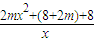 =
=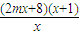 ,
,
∵x>0,∴x+1>0,
∴当m≥0时,8+2mx>0,F′(x)>0,此时,F(x)在(0,+∞)上是减函数,
当m<0时,由F′(x)>0得0<x<- ,由F′(x)<0得x>-
,由F′(x)<0得x>-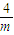 ,
,
此时,F(x)在(0,-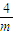 )上是增函数,在(-
)上是增函数,在(-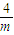 ,+∞)上是减函数,
,+∞)上是减函数,
综上所述,m≥0时,8+2mx>0,F′(x)>0,此时,F(x)在(0,+∞)上是减函数,当m<0时,由F′(x)>0得0<x<-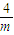 ,由F′(x)<0得x>-
,由F′(x)<0得x>-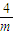 ,此时,F(x)在(0,-
,此时,F(x)在(0,-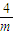 )上是增函数,在(-
)上是增函数,在(-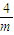 ,+∞)上是减函数,
,+∞)上是减函数,
(III)由条件(I)知, ,
,
假设曲线y=G(x)上存在两点P、Q,满足题意,则P、Q只能在y轴的同侧,
设P(t,G(t))(t>0),则Q(-t,t3+t2),
∵△OPQ(O为原点)是以O为直角顶点的直角三角形,
∴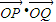 =0,即-t2+G(t)(t3+t2)=0,①
=0,即-t2+G(t)(t3+t2)=0,①
(1)当0<t≤2时,G(t)=-t3+t2,此时方程①为-t2+(-t3+t2)(t3+t2)=0,
化简得t4-t2+1=0,无解.满足条件的P、Q不存在;
(2)当t>2时,G(t)=aln(t-1),此时方程①为-t2+aln(t-1)(t3+t2)=0,
化简得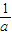 =(t+1)ln(t-1),设h(x)=(t+1)ln(t-1),则h′(x)=ln(t-1)+
=(t+1)ln(t-1),设h(x)=(t+1)ln(t-1),则h′(x)=ln(t-1)+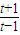 ,
,
当t>2时,h′(x)>0,h(x)在(2,+∞)上是增函数,h(x)的值域为(h(2),+∞),即(0,+∞).
∴当a>0时,方程①总有解.
综上所述,存在满足条件的P、Q,a的取值范围(0,+∞).
点评:本题考查利用导数研究函数的极值及单调性,解题时若含有参数,要对参数的取值进行讨论,而分类讨论的思想也是高考的一个重要思想,要注意体会其在解题中的运用.
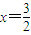 的对称点(1,0),由题意可得f(1)=0,求出m的值;
的对称点(1,0),由题意可得f(1)=0,求出m的值;(II)先求函数定义域,然后对函数求导,再对字母m分类讨论:当m≥0时,当m<0时.分别解f′(x)>0,f′(x)<0,求解即可.
(III)对于存在性问题,可先假设存在,即假设曲线y=G(x)上存在两点P、Q,满足题意,则P、Q只能在y轴的同侧,再利用△OPQ是以O为直角顶点的直角三角形,求出a的取值范围,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(I)令ln(x-1)=0,得x=2,∴点P关于直线
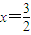 的对称点(1,0),
的对称点(1,0),∴f(1)=0,
 m+4+m=0,m=-3.
m+4+m=0,m=-3.(II)F(x)=f′(x)+g(x+1)mx2+2(4+m)x+8lnx,(x>0).
∴F′(x)=2mx+(8+2m)x+
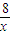 =
=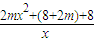 =
=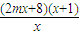 ,
,∵x>0,∴x+1>0,
∴当m≥0时,8+2mx>0,F′(x)>0,此时,F(x)在(0,+∞)上是减函数,
当m<0时,由F′(x)>0得0<x<-
 ,由F′(x)<0得x>-
,由F′(x)<0得x>-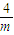 ,
,此时,F(x)在(0,-
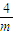 )上是增函数,在(-
)上是增函数,在(-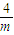 ,+∞)上是减函数,
,+∞)上是减函数,综上所述,m≥0时,8+2mx>0,F′(x)>0,此时,F(x)在(0,+∞)上是减函数,当m<0时,由F′(x)>0得0<x<-
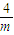 ,由F′(x)<0得x>-
,由F′(x)<0得x>-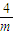 ,此时,F(x)在(0,-
,此时,F(x)在(0,-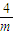 )上是增函数,在(-
)上是增函数,在(-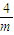 ,+∞)上是减函数,
,+∞)上是减函数,(III)由条件(I)知,
 ,
,假设曲线y=G(x)上存在两点P、Q,满足题意,则P、Q只能在y轴的同侧,
设P(t,G(t))(t>0),则Q(-t,t3+t2),
∵△OPQ(O为原点)是以O为直角顶点的直角三角形,
∴
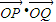 =0,即-t2+G(t)(t3+t2)=0,①
=0,即-t2+G(t)(t3+t2)=0,①(1)当0<t≤2时,G(t)=-t3+t2,此时方程①为-t2+(-t3+t2)(t3+t2)=0,
化简得t4-t2+1=0,无解.满足条件的P、Q不存在;
(2)当t>2时,G(t)=aln(t-1),此时方程①为-t2+aln(t-1)(t3+t2)=0,
化简得
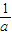 =(t+1)ln(t-1),设h(x)=(t+1)ln(t-1),则h′(x)=ln(t-1)+
=(t+1)ln(t-1),设h(x)=(t+1)ln(t-1),则h′(x)=ln(t-1)+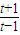 ,
,当t>2时,h′(x)>0,h(x)在(2,+∞)上是增函数,h(x)的值域为(h(2),+∞),即(0,+∞).
∴当a>0时,方程①总有解.
综上所述,存在满足条件的P、Q,a的取值范围(0,+∞).
点评:本题考查利用导数研究函数的极值及单调性,解题时若含有参数,要对参数的取值进行讨论,而分类讨论的思想也是高考的一个重要思想,要注意体会其在解题中的运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
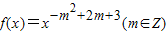 为偶函数,且在区间(0,+∞)上是单调增函数
为偶函数,且在区间(0,+∞)上是单调增函数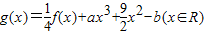 ,其中a,b∈R.若函数g(x)仅在x=0处有极值,求a的取值范围.
,其中a,b∈R.若函数g(x)仅在x=0处有极值,求a的取值范围.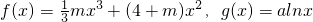 ,其中a≠0.
,其中a≠0.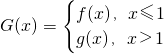 ,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由. ,其中a≠0.
,其中a≠0.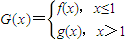 ,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.