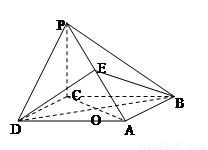题目内容
如图,四棱锥![]() 的底面是矩形,
的底面是矩形,![]() 底面
底面![]() ,P为BC边的中点,SB与平面ABCD所成的角为45°,且AD=2,SA=1.
,P为BC边的中点,SB与平面ABCD所成的角为45°,且AD=2,SA=1.
(1)求证:![]() 平面SAP;
平面SAP;
(2)求二面角A-SD-P的大小.
(2) ![]()
解析:
证明:(1)因为![]() 底面
底面![]() ,
,
所以,∠SBA是SB与平面ABCD所成的角…………………….……….1分
由已知∠SBA=45°,所以AB=SA=1
易求得,AP=PD=![]() ,…………………………………….…..………….2分
,…………………………………….…..………….2分
又因为AD=2,所以AD2=AP2+PD2,所以![]() .………….…….3分
.………….…….3分
因为SA⊥底面ABCD,![]() 平面ABCD,
平面ABCD,
所以SA⊥PD, …………….……………………….…....4分
由于SA∩AP=A 所以![]() 平面SAP. …………………………….5分
平面SAP. …………………………….5分
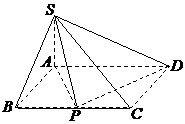
(2)设Q为AD的中点,连结PQ, ……………………………….………6分
 由于SA⊥底面ABCD,且SA
由于SA⊥底面ABCD,且SA![]() 平面SAD,则平面SAD⊥平面PAD……..7分
平面SAD,则平面SAD⊥平面PAD……..7分
因为PQ⊥AD,所以PQ⊥平面SAD
过Q作QR⊥SD,垂足为R,连结PR,
由三垂线定理可知PR⊥SD,
所以∠PRQ是二面角A-SD-P的平面角. …9分
容易证明△DRQ∽△DAS,则![]()
因为DQ=1,SA=1,![]() ,所以
,所以![]() ….……….10分
….……….10分
在Rt△PRQ中,因为PQ=AB=1,所以![]() ………11分
………11分
所以二面角A-SD-P的大小为![]() .……………….…….…….12分
.……………….…….…….12分
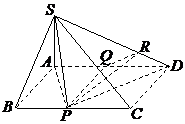
或:过A在平面SAP内作![]() ,且垂足为H,在平面SAD内作
,且垂足为H,在平面SAD内作![]() ,且垂足为E,连接HE,
,且垂足为E,连接HE,![]()
![]() 平面SAP。
平面SAP。![]()
![]() 平面SDP…………7分
平面SDP…………7分
∴HE为AE在平面SPD内的射影,∴由三垂线定理得![]()
从而![]() 是二面角A-SD-P的平面角……………………………….9分
是二面角A-SD-P的平面角……………………………….9分
在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,
,
![]()
![]() . ………………………………….11分
. ………………………………….11分
即二面角![]() 的大小为
的大小为![]() ……………………………12分
……………………………12分


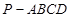 的底面是平行四边形,
的底面是平行四边形,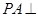 平面
平面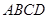 ,
,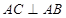 ,
,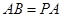 ,
,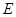 是
是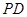 上的点,且
上的点,且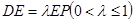 .
.
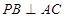 ;
; 的值,使
的值,使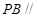 平面
平面 ;
;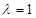 时,求三棱锥
时,求三棱锥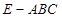 与四棱锥
与四棱锥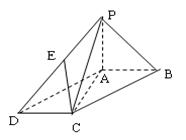
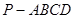 的底面
的底面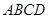 是正方形,侧棱
是正方形,侧棱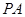
 底面
底面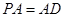 ,
, 、
、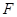 分别是棱
分别是棱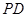 、
、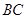 的中点.
的中点. 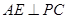 ; (2) 求直线
; (2) 求直线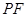 与平面
与平面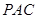 所成的角的正切值
所成的角的正切值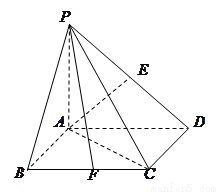
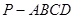 的底面是边长为
的底面是边长为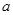 的菱形,
的菱形,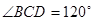 ,
,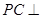 平面
平面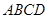 ,
,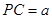 ,
, 为
为 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;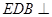 平面
平面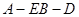 的正切值。
的正切值。