题目内容
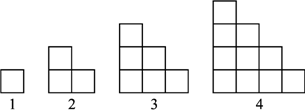
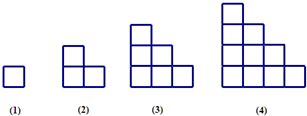
小正方形按照图中的规律排列,每个图形中的小正方形的个数构成数列{an}有以下结论,
(1)a5=15
(2){an}是一个等差数列;
(3)数列{an}是一个等比数列;
(4)数列{an}的递推公式an+1=an+n+1(n∈N*)
其中正确的是( )

(1)a5=15
(2){an}是一个等差数列;
(3)数列{an}是一个等比数列;
(4)数列{an}的递推公式an+1=an+n+1(n∈N*)
其中正确的是( )
分析:根据题意,结合等差数列的求和公式算出an=1+2+3+…+n=
,由此再对各个选项加以判断,可得(1)和(4)是真命题,而(2)(3)是假命题.
| n(n+1) |
| 2 |
解答:解:根据题意,可得
a1=1,a2=3=1+2,a3=6=1+2+3,a4=10=1+2+3+4,…
发现规律:an=1+2+3+…+n=
,
由此可得
a5=
=15,故(1)正确;{an}不是一个等差数列,故(2)不正确;
数列{an}不是一个等比数列,可得(3)不正确;
而an+1-an=
-
=
[(n+2)-n]=n+1
故an+1=an+n+1成立,故(4)正确
综上所述,正确命题为(1)(4)
故选:D
a1=1,a2=3=1+2,a3=6=1+2+3,a4=10=1+2+3+4,…
发现规律:an=1+2+3+…+n=
| n(n+1) |
| 2 |
由此可得
a5=
| 5(5+1) |
| 2 |
数列{an}不是一个等比数列,可得(3)不正确;
而an+1-an=
| (n+1)(n+2) |
| 2 |
| n(n+1) |
| 2 |
| n+1 |
| 2 |
故an+1=an+n+1成立,故(4)正确
综上所述,正确命题为(1)(4)
故选:D
点评:本题给出图形的特殊排列,叫我们依此判断命题的真假.着重考查了等差数列的通项与求和公式、数列递推式的推导等知识,属于中档题.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目