题目内容
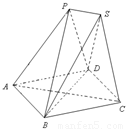
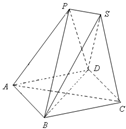 如图,已知放在同一平面上的两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等.若AB=6,二面角P-BD-S的余弦值为
如图,已知放在同一平面上的两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等.若AB=6,二面角P-BD-S的余弦值为| 1 | 3 |
(Ⅰ)求证:PB⊥平面PAD;
(Ⅱ)求多面体SPABC的体积..
分析:(I)设AC、BD的交点为O,连接OP、OS.先用等腰三角形PBD与等腰三角形SBD证明出PO、SO都与BO垂直,∠POS为二面角P-BD-S的平面角,然后在菱形ABCD中求出P、S在底面的射影的距离等于
2
,从而PS=2
,在等腰三角形PSO中利用余弦定理结合二面角P-BD-S的余弦值为
计算出PO长,再在Rt三角形POB中求出PB长,得到△PBD、△PBA都是等腰直角三角形,从而结合线面垂直的判定得到PB⊥平面PAD;
(II)根据(I)的数据不难计算出正三棱锥P-ABD的高PN=
,从而得到正三棱锥P-ABD的体积为9
,最终可得多面体SPABC的体积.
2
| 3 |
| 3 |
| 1 |
| 3 |
(II)根据(I)的数据不难计算出正三棱锥P-ABD的高PN=
| 6 |
| 2 |
解答:解:(Ⅰ)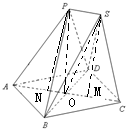 分别作出两个正三棱锥的高PN、SM,连接AC交BD于O,连接OP、OS
分别作出两个正三棱锥的高PN、SM,连接AC交BD于O,连接OP、OS
∵△ADB与△BCD都是正三角形
∴四边形ABCD是菱形且∠BCD=60°,可得AC、DB互相垂直平分
∵△PBD中,PB=PD,O为BD中点
∴PO⊥BD,
同理,SO⊥BD,可得∠POS为二面角P-BD-S的平面角
∵ON=
OA,OM=
OC∴MN=
AC
∵四边形ABCD是菱形且∠BCD=60°,
∴AC=
AB=6
⇒MN=
AC=2
∵正三棱锥P-ABD、S-BCD是两个全等的三棱锥
∴两条高PN、SM平行且相等
可得四边形PSMN是矩形,所以PS=MN=2
∵两个正三棱锥的侧棱长都相等
∴等腰三角形OPS中,根据余弦定理得:cos∠POS=
=
可得OP=OS=3
∵Rt△POB中,OB=
AB=3
∴PB=
=3
在△PDB中,PB2+PD2=36=BD2
∴∠BPD=90°⇒BP⊥PD
同理可得:BP⊥PA,结合PA∩PD=P
∴PB⊥平面PAD
(Ⅱ)由(I)得PA=PB=3
,AN=
AC=2
,
∴Rt△PAN中,高PN=
=
因此,正三棱锥P-ABD的体积V=
S △ABD•PN=
×
AB2×
=9
∴多面体SPABC的体积为V1=2×18
=18
 分别作出两个正三棱锥的高PN、SM,连接AC交BD于O,连接OP、OS
分别作出两个正三棱锥的高PN、SM,连接AC交BD于O,连接OP、OS∵△ADB与△BCD都是正三角形
∴四边形ABCD是菱形且∠BCD=60°,可得AC、DB互相垂直平分
∵△PBD中,PB=PD,O为BD中点
∴PO⊥BD,
同理,SO⊥BD,可得∠POS为二面角P-BD-S的平面角
∵ON=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∵四边形ABCD是菱形且∠BCD=60°,
∴AC=
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
∵正三棱锥P-ABD、S-BCD是两个全等的三棱锥
∴两条高PN、SM平行且相等
可得四边形PSMN是矩形,所以PS=MN=2
| 3 |
∵两个正三棱锥的侧棱长都相等
∴等腰三角形OPS中,根据余弦定理得:cos∠POS=
| OP2+OS2-PS2 |
| 2•OP•OS |
| 1 |
| 3 |
可得OP=OS=3
∵Rt△POB中,OB=
| 1 |
| 2 |
∴PB=
| OB2+OP2 |
| 2 |
在△PDB中,PB2+PD2=36=BD2
∴∠BPD=90°⇒BP⊥PD
同理可得:BP⊥PA,结合PA∩PD=P
∴PB⊥平面PAD
(Ⅱ)由(I)得PA=PB=3
| 2 |
| 1 |
| 3 |
| 3 |
∴Rt△PAN中,高PN=
| PA 2-AN2 |
| 6 |
因此,正三棱锥P-ABD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 6 |
| 2 |
∴多面体SPABC的体积为V1=2×18
| 3 |
| 2 |
点评:本题是一道立体几何的综合题,着重考查了组合几何体的面积、体积问题直线与平面垂直的判定等知识点,属于中档题.

练习册系列答案
相关题目
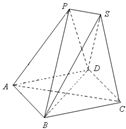 如图,已知放在同一平面上的两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等.若AB=6,二面角P-BD-S的余弦值为
如图,已知放在同一平面上的两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等.若AB=6,二面角P-BD-S的余弦值为 .
.
 .
.
 .
.