题目内容
数列{an}的前n项和Sn=n2+1是an=2n-1成立的
- A.充分但不必要条件
- B.必要但不充分条件
- C.充要条件
- D.既不充分又不必要条件
D
分析:先根据关系式:an= ,进行求解数列{an}的通项公式an,注意验证n=1时是否成立.最后看求出的通项公式与an=2n-1谁能推出谁即可.
,进行求解数列{an}的通项公式an,注意验证n=1时是否成立.最后看求出的通项公式与an=2n-1谁能推出谁即可.
解答:由题意知,当n=1时,a1=s1=1+1=2,
当n≥2时,an=sn-sn-1=(n2+1)-[(n-1)2+1)]=2n-1,
经验证当n=1时不符合上式,
∴an=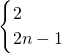
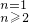 .
.
an=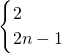
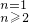 成立不能推出an=2n-1成立;
成立不能推出an=2n-1成立;
反之,an=2n-1成立也不能推出an=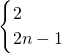
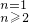 .
.
故选D.
点评:本题考查了必要条件、充分条件与充要条件的判断、数列通项公式和前n项和公式之间的关系式,即an= ,注意验证n=1时是否成立,这是容易忽视的地方.
,注意验证n=1时是否成立,这是容易忽视的地方.
分析:先根据关系式:an=
 ,进行求解数列{an}的通项公式an,注意验证n=1时是否成立.最后看求出的通项公式与an=2n-1谁能推出谁即可.
,进行求解数列{an}的通项公式an,注意验证n=1时是否成立.最后看求出的通项公式与an=2n-1谁能推出谁即可.解答:由题意知,当n=1时,a1=s1=1+1=2,
当n≥2时,an=sn-sn-1=(n2+1)-[(n-1)2+1)]=2n-1,
经验证当n=1时不符合上式,
∴an=
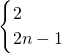
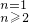 .
.an=
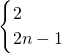
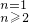 成立不能推出an=2n-1成立;
成立不能推出an=2n-1成立;反之,an=2n-1成立也不能推出an=
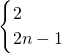
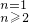 .
.故选D.
点评:本题考查了必要条件、充分条件与充要条件的判断、数列通项公式和前n项和公式之间的关系式,即an=
 ,注意验证n=1时是否成立,这是容易忽视的地方.
,注意验证n=1时是否成立,这是容易忽视的地方. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目