题目内容
若椭圆E1: 和椭圆E2:
和椭圆E2: 满足
满足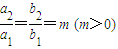 ,则称这两个椭圆相似,m称为其相似比.
,则称这两个椭圆相似,m称为其相似比.(1)求经过点
 ,且与椭圆
,且与椭圆 相似的椭圆方程;
相似的椭圆方程;(2)设过原点的一条射线l分别与(1)中的两个椭圆交于A、B两点(其中点A在线段OB上),
求
 的最大值和最小值;
的最大值和最小值;(3)对于真命题“过原点的一条射线分别与相似比为2的两个椭圆C1:
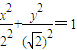 和C2:
和C2: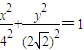 交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为
交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为 ”.请用推广或类比的方法提出类似的一个真命题,并给予证明.
”.请用推广或类比的方法提出类似的一个真命题,并给予证明.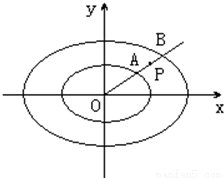
【答案】分析:(1)直接根据定义得到有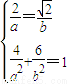 解得
解得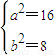 即可得到与椭圆
即可得到与椭圆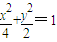 相似的椭圆方程;
相似的椭圆方程;
(2)先对射线与y轴重合时求出结论;再对射线不与坐标轴重合时,由椭圆的对称性,仅考查A、B在第一象限的情形,联立直线与两个椭圆方程分别求出线段的长度,再结合函数的单调性即可求出 的最大值和最小值;(整理过程需小心避免出错).
的最大值和最小值;(整理过程需小心避免出错).
(3)分析出命题的基本条件为:椭圆、 、m=2、等差,类比着写:①双曲线或抛物线; ②a,b或p; ③相似比为m;④等比,再加以证明即可.
、m=2、等差,类比着写:①双曲线或抛物线; ②a,b或p; ③相似比为m;④等比,再加以证明即可.
解答: 解:(1)设所求的椭圆方程为
解:(1)设所求的椭圆方程为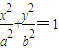 ,则有
,则有 解得
解得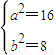
∴所要求的椭圆方程为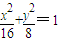
(2)①当射线与y轴重合时,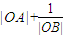 =
=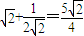
②当射线不与坐标轴重合时,由椭圆的对称性,我们仅考察A、B在第一象限的情形.
设其方程为y=kx(k≥0,x>0),设A(x1,y1),B(x2,y2)
由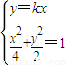 解得
解得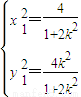

由 解得
解得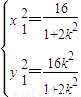 ,
,
∴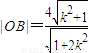
∴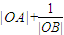 =
=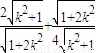
令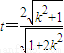 则由
则由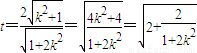 知
知
∴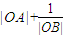 =
=
记 ,则f(t)在
,则f(t)在 上是增函数,∴
上是增函数,∴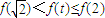 ,
,
∴
由①②知,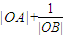 的最大值为
的最大值为 ,
, 的最小值为
的最小值为 .
.
(3)本题根据学生提出和解决问题的质量评分
命题结构:条件⇒结论
条件由四部分组成:

其中基本条件为:椭圆、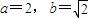 、m=2、等差,
、m=2、等差,
得分条件为:①双曲线或抛物线; ②a,b或p; ③相似比为m;④等比.
例1:①双曲线+②a,b+③相似比为m+等差
过原点的一条射线分别与两条双曲线C1: 和C2:
和C2: (m>0)交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为
(m>0)交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为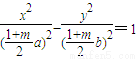
证明:∵射线l与双曲线有交点,不妨设其斜率为k,显然 .
.
设射线l的方程为y=kx,设点A(x1,y1)、B(x2,y2)、p(x,y)
由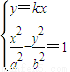 解得
解得 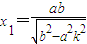 ,
,
由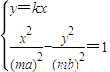 解得
解得 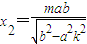
由P点在射线l上,且2|OP|=|OA|+|OB|得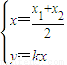 即
即
得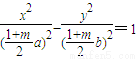
例2:①抛物线+②p+③相似比为m+等差
过原点的一条射线分别与两条抛物线C1:y2=2px(p>0)和C2:y2=2mpx(m>0)相交于异于原点的A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为y2=(1+m)px
证明:∵射线l与抛物线有异于原点的交点,不妨设其斜率为k.
设射线l的方程为y=kx,设点A(x1,y1)、B(x2,y2)、p(x,y)
由 解得
解得 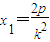 ,
,
由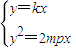 解得
解得 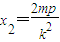
由P点在射线l上,且2|OP|=|OA|+|OB|得 即
即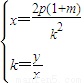
得 y2=(1+m)px
点评:本题综合考查直线和椭圆的位置关系,难度较大,解题时要仔细审题,注意公式的灵活运用.
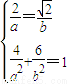 解得
解得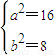 即可得到与椭圆
即可得到与椭圆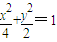 相似的椭圆方程;
相似的椭圆方程;(2)先对射线与y轴重合时求出结论;再对射线不与坐标轴重合时,由椭圆的对称性,仅考查A、B在第一象限的情形,联立直线与两个椭圆方程分别求出线段的长度,再结合函数的单调性即可求出
 的最大值和最小值;(整理过程需小心避免出错).
的最大值和最小值;(整理过程需小心避免出错).(3)分析出命题的基本条件为:椭圆、
 、m=2、等差,类比着写:①双曲线或抛物线; ②a,b或p; ③相似比为m;④等比,再加以证明即可.
、m=2、等差,类比着写:①双曲线或抛物线; ②a,b或p; ③相似比为m;④等比,再加以证明即可.解答:
 解:(1)设所求的椭圆方程为
解:(1)设所求的椭圆方程为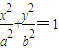 ,则有
,则有 解得
解得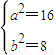
∴所要求的椭圆方程为
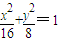
(2)①当射线与y轴重合时,
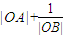 =
=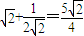
②当射线不与坐标轴重合时,由椭圆的对称性,我们仅考察A、B在第一象限的情形.
设其方程为y=kx(k≥0,x>0),设A(x1,y1),B(x2,y2)
由
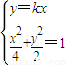 解得
解得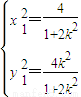

由
 解得
解得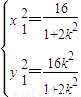 ,
,∴
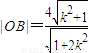
∴
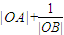 =
=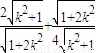
令
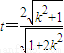 则由
则由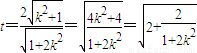 知
知
∴
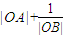 =
=
记
 ,则f(t)在
,则f(t)在 上是增函数,∴
上是增函数,∴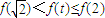 ,
,∴

由①②知,
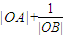 的最大值为
的最大值为 ,
, 的最小值为
的最小值为 .
.(3)本题根据学生提出和解决问题的质量评分
命题结构:条件⇒结论
条件由四部分组成:

其中基本条件为:椭圆、
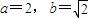 、m=2、等差,
、m=2、等差,得分条件为:①双曲线或抛物线; ②a,b或p; ③相似比为m;④等比.
例1:①双曲线+②a,b+③相似比为m+等差
过原点的一条射线分别与两条双曲线C1:
 和C2:
和C2: (m>0)交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为
(m>0)交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为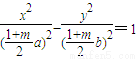
证明:∵射线l与双曲线有交点,不妨设其斜率为k,显然
 .
.设射线l的方程为y=kx,设点A(x1,y1)、B(x2,y2)、p(x,y)
由
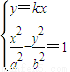 解得
解得 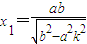 ,
,由
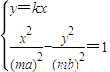 解得
解得 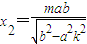
由P点在射线l上,且2|OP|=|OA|+|OB|得
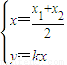 即
即
得
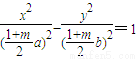
例2:①抛物线+②p+③相似比为m+等差
过原点的一条射线分别与两条抛物线C1:y2=2px(p>0)和C2:y2=2mpx(m>0)相交于异于原点的A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为y2=(1+m)px
证明:∵射线l与抛物线有异于原点的交点,不妨设其斜率为k.
设射线l的方程为y=kx,设点A(x1,y1)、B(x2,y2)、p(x,y)
由
 解得
解得 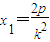 ,
,由
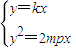 解得
解得 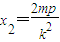
由P点在射线l上,且2|OP|=|OA|+|OB|得
 即
即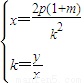
得 y2=(1+m)px
点评:本题综合考查直线和椭圆的位置关系,难度较大,解题时要仔细审题,注意公式的灵活运用.

练习册系列答案
相关题目
 如图,已知椭圆E1方程为
如图,已知椭圆E1方程为 ,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.  ,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值; 时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
 ,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.  ,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值; 时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.