题目内容
某隧道长2150m,通过隧道的车速不能超过20m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s)匀速通过该隧道,设车队的速度为xm/s,根据安全和车流的需要,当0<x≤10时,相邻两车之间保持20m的距离;当10<x≤20时,相邻两车之间保持(
x2+
x)m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为y(s).
(1)将y表示为x的函数;
(2)求车队通过隧道时间y的最小值及此时车队的速度.(
≈1.73)
| 1 |
| 6 |
| 1 |
| 3 |
(1)将y表示为x的函数;
(2)求车队通过隧道时间y的最小值及此时车队的速度.(
| 3 |
(1)当0<x≤10时,y=
=
,
当10<x≤20时,y=
=
+9x+18,
所以,y=
,
(2)当x∈(0,10]时,在x=10时,ymin=
=378(s),
当x∈(10,20]时,y=
+9x+18≥18+2×
=18+180
≈329.4(s),
当且仅当9x=
,即:x≈17.3(m/s)时取等号.
因为17.3∈(10,20],所以当x=17.3(m/s)时,ymin=329.4(s),
而378>329.4,
所以,当车队的速度为17.3(m/s)时,车队通过隧道时间y有最小值329.4(s).
| 2150+10×55+20×(55-1) |
| x |
| 3780 |
| x |
当10<x≤20时,y=
2150+10×55+(
| ||||
| x |
| 2700 |
| x |
所以,y=
|
(2)当x∈(0,10]时,在x=10时,ymin=
| 3780 |
| 10 |
当x∈(10,20]时,y=
| 2700 |
| x |
9x•
|
| 3 |
当且仅当9x=
| 2700 |
| x |
因为17.3∈(10,20],所以当x=17.3(m/s)时,ymin=329.4(s),
而378>329.4,
所以,当车队的速度为17.3(m/s)时,车队通过隧道时间y有最小值329.4(s).

练习册系列答案
相关题目


 是方程
是方程 (
( 是实常数)
是实常数) 的一个根,
的一个根, 是
是 的反函数,则方程
的反函数,则方程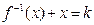 必有一根是 .
必有一根是 . 的结果是( )
的结果是( )
