题目内容
(1)设全集为R,集合A={x|3≤x<7},集合B={x|2<x<8},求(CRA)∩B.
(2)已知集合A={x|x2-x-2=0},B={x|ax-1=0},若A∪B=A,求实数a的值组成的集合.
(2)已知集合A={x|x2-x-2=0},B={x|ax-1=0},若A∪B=A,求实数a的值组成的集合.
分析:(1)求出CRA,然后通过CRA求解(CRA)∩B.
(2)由条件可得B⊆A,分a=0和a≠0,分别求出B,再由B⊆A,求得a的值,即可得到实数a的值所组成的集合.
(2)由条件可得B⊆A,分a=0和a≠0,分别求出B,再由B⊆A,求得a的值,即可得到实数a的值所组成的集合.
解答:解:(1)CRA={x|x<3,或x≥7}------------------------(3分)
(CRA)∩B={x|2<x<3,或7≤x<8}----------(7分)
(2)由题意得A={-1,2},B⊆A------------------------(2分)
当a=0时,A=φ,满足题意;------------------------(4分)
当a≠0时,B={x|x=
},由B⊆A得
=-1或2
解得a=-1或a=
------------------------(6分)
综上,实数a的值组成的集合为{-1, 0,
}------------------------(7分)
(CRA)∩B={x|2<x<3,或7≤x<8}----------(7分)
(2)由题意得A={-1,2},B⊆A------------------------(2分)
当a=0时,A=φ,满足题意;------------------------(4分)
当a≠0时,B={x|x=
| 1 |
| a |
| 1 |
| a |
解得a=-1或a=
| 1 |
| 2 |
综上,实数a的值组成的集合为{-1, 0,
| 1 |
| 2 |
点评:本题考查交、并、补集的混合运算,考查集合关系中参数的取值范围问题,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
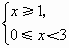 的解集为A,则
的解集为A,则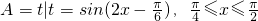 ,若不等式t2+at+b≤0的解集是A,求a,b的值.
,若不等式t2+at+b≤0的解集是A,求a,b的值.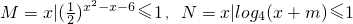 ,若M∩N=Φ,求实数m的取值范围.
,若M∩N=Φ,求实数m的取值范围.