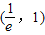Question

曲线C：y=e^x在点A处的切线l恰好经过坐标原点，则A点的坐标为（ ）
A．（1，e）
B．（1，1）
C．（e，1）
D．

Answer 1

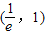
【答案】分析：设出点A的坐标，求出切线方程，将（0，0）代入，可得结论．
解答：解：设A（a，e^a），则∵y=e^x，∴y′=e^x，
∴x=a时，y′=e^a，
∴曲线C：y=e^x在点A处的切线l的方程为y-e^a=e^a（x-a）
将（0，0）代入，可得0-e^a=e^a（0-a）
∴a=1，∴A点的坐标为（1，e）
故选A．
点评：本题考查导数知识的运用，考查导数的几何意义，属于基础题．