题目内容
已知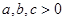 , 且
, 且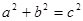 ,求证:
,求证: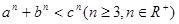
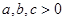 , 且
, 且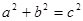 ,求证:
,求证: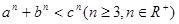
运用两个正数的平方和为1,说明了各自都是小于1的,然后借助于指数函数的单调性放缩得到证明。
试题分析:证如下:
∵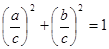 ,
,
又a, b, c > 0,
∴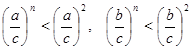
∴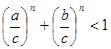
点评:对于不等式的证明,可以构造函数来结合函数的单调性来得到不等式的关系,也可以直接运用均值不等式来放缩得到结论,有难度的试题。
试题分析:证如下:
∵
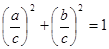 ,
,又a, b, c > 0,
∴
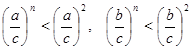
∴
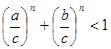
点评:对于不等式的证明,可以构造函数来结合函数的单调性来得到不等式的关系,也可以直接运用均值不等式来放缩得到结论,有难度的试题。

练习册系列答案
相关题目
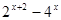
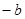 =0.
=0.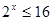 且
且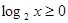 ,求实数b的取值范围.
,求实数b的取值范围.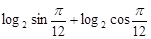 的值为 .
的值为 .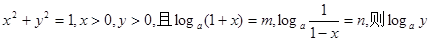 等于( )
等于( )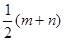
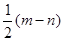
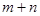
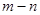
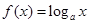
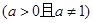 在
在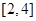 上的最大值与最小值之差为2,则
上的最大值与最小值之差为2,则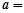 .
.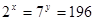 ,则
,则 。
。 ;
; 求
求 的值.
的值. 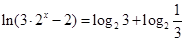 的解为
的解为