题目内容
如果抛物线y=x2-2xsinθ+1的顶点在椭圆x2+4y2=1上，则这样的抛物线共有分析：求出抛物线的顶点坐标，代入椭圆方程，求出sinθ的值的个数，即可解得抛物线的条数．
解答：解：抛物线y=x2-2xsinθ+1可得顶点（sinθ，cos2θ）
代入椭圆方程得：
sin2θ+4cos4θ=1
4cos4θ=cos2θ
cos2θ=0或cos2θ=
对应的sinθ有4个不同的值，
所以，这样的抛物线共有4条
故答案为：4
代入椭圆方程得：
sin2θ+4cos4θ=1
4cos4θ=cos2θ
cos2θ=0或cos2θ=
| 1 |
| 4 |
对应的sinθ有4个不同的值，
所以，这样的抛物线共有4条
故答案为：4
点评：本题是基础题，考查抛物线的顶点坐标的求法，三角函数方程的求法，考查计算能力．
练习册系列答案
相关题目
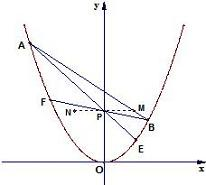已知抛物线y=x2和三个点M（x0，y0）、P（0，y0）、N（-x0，y0）（y0≠x02，y0＞0），过点M的一条直线交抛物线于A、B两点，AP、BP的延长线分别交曲线C于E、F．