题目内容
如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=2a,CD=a,F是BE的中点.
(1)求证:DF∥平面ABC;
(2)求证:AF⊥BD.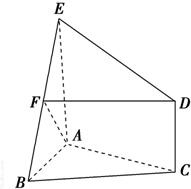
(1)求证:DF∥平面ABC;
(2)求证:AF⊥BD.

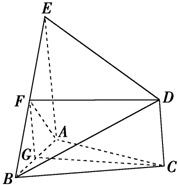
证明:(1)取AB的中点G,连接FG,可得FG∥AE,FG=
| 1 |
| 2 |
又CD⊥平面ABC,AE⊥平面ABC,
∴CD∥AE,CD=
| 1 |
| 2 |
∴FG∥CD,FG=CD,
∵FG⊥平面ABC,
∴四边形CDFG是矩形,DF∥CG,
CG?平面ABC,DF?平面ABC,
∴DF∥平面ABC.
(2)Rt△ABE中,AE=2a,AB=2a,
F为BE中点,∴AF⊥BE,
∵△ABC是正三角形,∴CG⊥AB,
∴DF⊥AB,
又DF⊥FG,
∴DF⊥平面ABE,DF⊥AF,
∴AF⊥平面BDF,∴AF⊥BD.

练习册系列答案
相关题目
 如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=2a,CD=a,F是BE的中点.
如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=2a,CD=a,F是BE的中点. 如图所示,△ABC是等腰直角三角形,AC=BC=a,P是△ABC所在平面外一点,
如图所示,△ABC是等腰直角三角形,AC=BC=a,P是△ABC所在平面外一点, 如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=2DC,F是BE的中点.求证:
如图所示,△ABC是正三角形,AE和CD都垂直于平面ABC,且AE=AB=2DC,F是BE的中点.求证:
