Question

某生产饮料的企业拟投入适当的广告费对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系为Q=(x≥0).已知生产此产品的年固定投入为3万元,每生产1万件此产品需再投入32万元.若每件售价为“年平均每件成本的150%”与“年平均每件所占广告费的50%”之和.

(1)试将利润y(万元)表示为年广告费x(万元)的函数.如果年广告费投入100万元,企业是亏损还是盈利?

(2)当年广告费投入多少万元时,企业年利润最大?

Answer 1

解：(1)由题意,每年产销Q万件,共计成本为(32Q+3)万元.

销售收入是(32Q+3)·150%+x·50%.

∴年利润y=年收入-年成本-年广告费

=(32Q+3-x)=(32×+3-x)

∴所求的函数关系式为y=

当x=100时,y＜0,故当年广告费投入100万元时,企业亏损.

(2)由y=，可得

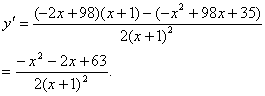
令y′=0,则x²+2x-63=0,∴x=-9(舍去)或x=7.

又x∈(0,7)时,y′＞0;x∈(7,+∞)时,y′＜0,

∴y_极大值=42.

又∵在(0,+∞)上只有一个极值点,

∴y_max=y_极大值=42.

故当年广告费投入7万元时,企业年利润最大,最大利润为42万元.