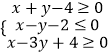题目内容
【题目】已知f（x）=x5 
+bx﹣8，且f（﹣2）=10，则f（2）=（ ）
A.﹣26
B.﹣18
C.﹣10
D.10
【答案】A
【解析】解：设f（x）=x5 
+bx﹣8=g（x）﹣8，∴g（x）为奇函数，
由f（﹣2）=g（﹣2）﹣8=10，可得g（﹣2）=﹣g（2）=18，故g（2）=﹣18．
则f（2）=g（2）﹣8=﹣18﹣8=﹣26，
所以答案是：A．
【考点精析】关于本题考查的函数奇偶性的性质，需要了解在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇才能得出正确答案．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某企业生产甲、乙两种产品均需用A，B两种原料．已知生产1吨每种产品所需原料及每天原料的可用限额如表所示．如果生产一吨甲、乙产品可获得利润分别为3万元、4万元，则该企业每天可获得最大利润为（ ）
甲 | 乙 | 原料限额 | |
A（吨） | 3 | 2 | 12 |
B（吨） | 1 | 2 | 8 |
A.12万元
B.16万元
C.17万元
D.18万元
