题目内容
2.已知|$\overrightarrow{a}$|=6,|$\overrightarrow{b}$|=8,$\overrightarrow{a}•\overrightarrow{b}$=0,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则$\overrightarrow{a}•\overrightarrow{c}$的最大值是60.分析 由已知|$\overrightarrow{a}$|=6,|$\overrightarrow{b}$|=8,$\overrightarrow{a}•\overrightarrow{b}$=0,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0展开得到${\overrightarrow{c}}^{2}=(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{c}$,又|$\overrightarrow{a}+\overrightarrow{b}$|=10,设$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{c}$夹角为θ,得到|$\overrightarrow{c}$|=10cosθ,得到其最大值为10,进一步设$\overrightarrow{a}$,$\overrightarrow{c}$的夹角为α,利用数量积公式得到所求最大值.
解答 解:因为|$\overrightarrow{a}$|=6,|$\overrightarrow{b}$|=8,$\overrightarrow{a}•\overrightarrow{b}$=0,向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,所以${\overrightarrow{c}}^{2}=(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{c}$,又|$\overrightarrow{a}+\overrightarrow{b}$|=10,设$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{c}$夹角为θ,得到|$\overrightarrow{c}$|=10cosθ,
所以|$\overrightarrow{c}$|的最大值为10,
设$\overrightarrow{a}$,$\overrightarrow{c}$的夹角为α,则$\overrightarrow{a}•\overrightarrow{c}$=|$\overrightarrow{a}$||$\overrightarrow{c}$|cosα≤|$\overrightarrow{a}$||$\overrightarrow{c}$|=60;
故答案为:60.
点评 本题考查平面向量数量积的运算,属中档题,熟练掌握相关运算性质是解题基.

 阅读快车系列答案
阅读快车系列答案| A. | -1 | B. | 2 | C. | 2或-1 | D. | 0或-1 |
| A. | 345° | B. | -345° | C. | 235° | D. | -435° |
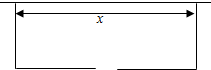 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).