题目内容
将函数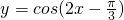 的图象向左平移
的图象向左平移 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得函数图象的一条对称轴是
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得函数图象的一条对称轴是
- A.

- B.

- C.x=π
- D.x=

C
分析:根据函数y=Asin(ωx+∅)的图象变换规律求出所得函数图象的解析式为 y=cosx,可得其对称轴为 x=kπ,k∈z,从而得到答案.
解答:将函数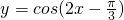 的图象向左平移
的图象向左平移 个单位得到函数y=
个单位得到函数y=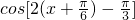 =cos2x的图象,
=cos2x的图象,
再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得函数图象对应的函数解析式为 y=cosx,其对称轴为 x=kπ,k∈z,
故选C.
点评:本题主要考查余弦函数的对称性,函数y=Asin(ωx+∅)的图象变换规律,属于中档题.
分析:根据函数y=Asin(ωx+∅)的图象变换规律求出所得函数图象的解析式为 y=cosx,可得其对称轴为 x=kπ,k∈z,从而得到答案.
解答:将函数
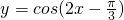 的图象向左平移
的图象向左平移 个单位得到函数y=
个单位得到函数y=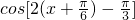 =cos2x的图象,
=cos2x的图象,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得函数图象对应的函数解析式为 y=cosx,其对称轴为 x=kπ,k∈z,
故选C.
点评:本题主要考查余弦函数的对称性,函数y=Asin(ωx+∅)的图象变换规律,属于中档题.

练习册系列答案
相关题目
 下列结论:
下列结论: 的最小正周期是
的最小正周期是 ;
; 上单调递增;
上单调递增; 成中心对称图形;
成中心对称图形; 个单位后与
个单位后与 的图象重合;
的图象重合; 的图象向左平移
的图象向左平移 个长度单位,再保持所有点的纵坐标不变横坐标压缩为原来的
个长度单位,再保持所有点的纵坐标不变横坐标压缩为原来的 ,得到函数
,得到函数 的图象,则使
的图象,则使 B.
B.  C.
C.  D.
D. 
 的图象向左平移m(m>0)个单位,若所得图象对应的函数为偶函数,则m的最小值是( )
的图象向左平移m(m>0)个单位,若所得图象对应的函数为偶函数,则m的最小值是( ) B.
B. C.
C. D.
D.