题目内容
(2013•金山区一模)若函数y=f(x) (x∈R)满足:f(x+2)=f(x),且x∈[-1,1]时,f(x)=|x|,函数y=g(x)是定义在R上的奇函数,且x∈(0,+∞)时,g(x)=log 3x,则函数y=f(x)的图象与函数y=g(x)的图象的交点个数为
4
4
.分析:函数f(x)满足f(x+2)=f(x)知f(x)是周期函数,当x∈[-1,1]时,f(x)=|x|,可以画出f(x)的图象;又函数g(x)是R上的奇函数,且x∈(0,+∞),g(x)=log 3x,讨论x>0,x=0,x<0时,f(x)与g(x)图象交点的情况.
解答: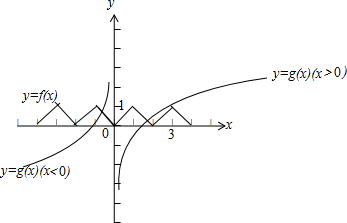 解:函数y=f(x) (x∈R)满足:f(x+2)=f(x),
解:函数y=f(x) (x∈R)满足:f(x+2)=f(x),
∴f(x)是以2为周期的函数;
当x∈[-1,1]时,f(x)=|x|,可以画出f(x)的图象如下;
又函数y=g(x)是定义在R上的奇函数,且x∈(0,+∞)时,g(x)=log 3x,
∵x=3时,g(3)=1,∴当x>0时,f(x)与g(x)的图象有两个交点;
当x=0时,f(0)=g(0)=0,∴f(x)与g(x)的图象有一个交点;
当x<0时,g(x)是R上的奇函数,
∴g(x)=-g(-x)=-log3(-x)=log3
,与y=f(x)的图象有一个交点;
如图所示:所以,函数y=f(x)与y=g(x)的图象的交点有4个.
故答案为:4.
 解:函数y=f(x) (x∈R)满足:f(x+2)=f(x),
解:函数y=f(x) (x∈R)满足:f(x+2)=f(x),∴f(x)是以2为周期的函数;
当x∈[-1,1]时,f(x)=|x|,可以画出f(x)的图象如下;
又函数y=g(x)是定义在R上的奇函数,且x∈(0,+∞)时,g(x)=log 3x,
∵x=3时,g(3)=1,∴当x>0时,f(x)与g(x)的图象有两个交点;
当x=0时,f(0)=g(0)=0,∴f(x)与g(x)的图象有一个交点;
当x<0时,g(x)是R上的奇函数,
∴g(x)=-g(-x)=-log3(-x)=log3
| 1 |
| -x |
如图所示:所以,函数y=f(x)与y=g(x)的图象的交点有4个.
故答案为:4.
点评:本题考查了函数的周期性,奇偶性,对数函数以及函数图象的综合应用,是一个容易出错的题目.

练习册系列答案
相关题目