Question

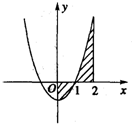由曲线y=x²-1，直线x=0，x=2和x轴围成的封闭图形的面积（如图）可表示为（　　）

• A．

  ∫

  2 0

  (x2-1)dx
• B．

  ∫

  2 0

  |x2-1|dx
• C．|

  ∫

  2 0

  (x2-1)dx|
• D．

  ∫

  2 0

  (x2-1)dx+

  ∫

  2 1

  (x2-1)dx

Answer 1

分析：将函数y=x²-1的图象进行变换，得函数y=|x²-1|的图象．根据全等图形的面积相等，可得曲线y=x²-1，直线x=0，x=2和x轴围成的封闭图形的面积，恰好等于函数y=|x²-1|在[0，2]上的图象投影到x轴所成的面积，得到本题的答案．

解答：解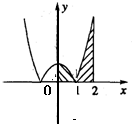：将函数y=x²-1的图象位于x轴下方的部分对称到x轴的上方，
而x轴上方的部分不变，得函数y=|x²-1|的图象
可得曲线y=x²-1，直线x=0，x=2和x轴围成的封闭图形的面积，
恰好等于函数y=|x²-1|在[0，2]上的图象投影到x轴所成的面积，如图中的阴影部分．
∴所求的阴影部分面积S=

∫

2 0

|x2-1|dx
故选：B

点评：本题给出曲线y=x²-1与x=0，x=2和x轴围成的图形，要我们找出等于这个面积的积分值，着重考查了基本初等函数图象的变换和定积分的几何意义等知识，属于基础题．