题目内容
(本小题满分l4分)
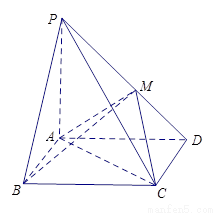
如图4,在四棱锥 中,底面
中,底面 是矩形,
是矩形,
 平面
平面 ,
, ,
, ,
,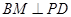 于点
于点 .
.
(1) 求证:
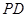 ;
;
(2) 求直线 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.
【答案】
(1)证明:∵  平面
平面 ,
, 平面
平面 ,∴
,∴ .
.
∵ ,
, 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .
.
∵ 平面
平面
∴ ,
……3分
,
……3分
∵ ,
,  ,
, 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴
 .
……6分
.
……6分
(2)解法1:由(1)知, ,又
,又 ,
,
则 是
是 的中点,
的中点,
在Rt△ 中,得
中,得 ,在Rt△
,在Rt△ 中,得
中,得 ,
,
∴ .
.
设点 到平面
到平面 的距离为
的距离为 ,由
,由 , ……8分
, ……8分
得 .
.
解得 ,
……10分
,
……10分
设直线 与平面
与平面 所成的角为
所成的角为 ,则
,则 , …12分
, …12分
∴ .
.
∴ 直线 与平面
与平面 所成的角的余弦值为
所成的角的余弦值为 . ……14分
. ……14分
解法2: 如图所示,以点 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系 ,
,
则 ,
, ,
, ,
, ,
, ,
, .
.
∴ .
……8分
.
……8分
设平面 的一个法向量为
的一个法向量为 ,
,
由 可得:
可得:
令 ,得
,得 .
.
∴ .
……10分
.
……10分
设直线 与平面
与平面 所成的角为
所成的角为 ,则
,则 . 12分
. 12分
∴ .
.
∴直线 与平面
与平面 所成的角的余弦值为
所成的角的余弦值为 . ……14分
. ……14分
【解析】略

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 ,
, (
( )
) ,证明:
,证明: .
. 的正方体
的正方体 中,
中, 是
是 的中点,
的中点, 在线段
在线段 上,且
上,且 .
. 与
与 所成角的余弦值;
所成角的余弦值; 面
面 ;
; 到面
到面
 有唯一的零点
有唯一的零点 .
.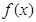 的表达式;
的表达式; 上具有单调性,求实数
上具有单调性,求实数 的取值范围;
的取值范围; (其中
(其中 )的图象如下图所示。
)的图象如下图所示。
 ,
, 及
及 的值;
的值;
 ,且
,且 ,求
,求 的值.。
的值.。