题目内容
若正实数a,b满足ln(a+b)=0,则
+
的最小值为 .
| 1 |
| a |
| 2 |
| b |
分析:根据对数的运算,由ln(a+b)=0求出a+b=1,利用“1”的代换的思想,将
+
转化为(
+
)(a+b),展开后利用基本不等式,即可求得答案.
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
解答:解:∵ln(a+b)=0,
∴ln(a+b)=ln1,
∴a+b=1,
又∵a,b为正实数,
∴
+
=(
+
)(a+b)=
+
+3≥2
+3=2
+3,
当且仅当
=
,即a=
-1,b=2-
时取等号,
∴
+
的最小值为2
+3.
故答案为:2
+3.
∴ln(a+b)=ln1,
∴a+b=1,
又∵a,b为正实数,
∴
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 2a |
| b |
|
| 2 |
当且仅当
| b |
| a |
| 2a |
| b |
| 2 |
| 2 |
∴
| 1 |
| a |
| 2 |
| b |
| 2 |
故答案为:2
| 2 |
点评:本题考查了基本不等式在最值问题中的应用.运用基本不等式求最值时要注意“一正、二定、三相等”的判断.本题运用了“1”的代换的思想,解题的关键是将常数1代换为a+b,构造出乘积为最值的求和形式.属于中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
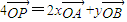 ,则
,则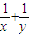 的最小值为 .
的最小值为 . (其中tanθ=2,θ为锐角)作平行于
(其中tanθ=2,θ为锐角)作平行于 的直线l与曲线分别交于B,C.
的直线l与曲线分别交于B,C. ;
;