题目内容
已知平面内一动点P到点F（1，0）的距离与点P到y轴的距离的差等于1．（1）求动点P的轨迹C的方程．
（2）过点F作两条斜率存在且互相垂直的直线l1、l2，设l1与轨迹C交于A、B两点，l2与轨迹C交于D、E两点，求|FA|•|FB|+|FC|•|FD|的最小值．
【答案】分析：（1）根据平面内一动点P到点F（1，0）的距离与点P到y轴的距离的差等于1，可得当x≥0时，点P到F的距离等于点P到直线x=-1的距离，所以动点P的轨迹为抛物线；当x＜0时，y=0也满足题意；
（2）设l1的方程为y=k（x-1）与抛物线方程联立，设A（x1，y1），B（x2，y2），利用韦达定理可得x1+x2=2+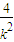
，x1x2=1，x3+x4=2+4k2，x3x4=1，从而可得|FA||FB|+|FD||FE|=8+4（k2+
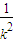）≥16，由此即可得到结论．
解答：解：（1）∵平面内一动点P到点F（1，0）的距离与点P到y轴的距离的差等于1
∴当x≥0时，点P到F的距离等于点P到直线x=-1的距离，
∴动点P的轨迹为抛物线，方程为y2=4x（x≥0）
当x＜0时，y=0
∴动点P的轨迹C的方程为y2=4x（x≥0）或y=0（x＜0）
（2）由题意知，直线l1的斜率存在且不为0，设为k，则l1的方程为y=k（x-1）
与抛物线方程联立，消元可得k2x2-（2k2+4）x+k2=0
设A（x1，y1），B（x2，y2），则x1，x2是上述方程的两个实根，所以x1+x2=2+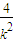
，x1x2=1
∵l1⊥l2，∴l2的斜率为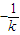
设D（x3，y3），E（x4，y4），则同理可得x3+x4=2+4k2，x3x4=1
∴|FA||FB|+|FD||FE|=（x1+1）（x2+1）+（x3+1）（x4+1）=8+4（k2+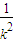
）≥16（当且仅当k=±1时取等号）
∴|FA|•|FB|+|FC|•|FD|的最小值为16．
点评：本题考查轨迹方程，考查直线与抛物线的位置关系，解题的关键是确定抛物线的方程，利用韦达定理解题．
（2）设l1的方程为y=k（x-1）与抛物线方程联立，设A（x1，y1），B（x2，y2），利用韦达定理可得x1+x2=2+
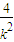，x1x2=1，x3+x4=2+4k2，x3x4=1，从而可得|FA||FB|+|FD||FE|=8+4（k2+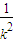）≥16，由此即可得到结论．解答：解：（1）∵平面内一动点P到点F（1，0）的距离与点P到y轴的距离的差等于1
∴当x≥0时，点P到F的距离等于点P到直线x=-1的距离，
∴动点P的轨迹为抛物线，方程为y2=4x（x≥0）
当x＜0时，y=0
∴动点P的轨迹C的方程为y2=4x（x≥0）或y=0（x＜0）
（2）由题意知，直线l1的斜率存在且不为0，设为k，则l1的方程为y=k（x-1）
与抛物线方程联立，消元可得k2x2-（2k2+4）x+k2=0
设A（x1，y1），B（x2，y2），则x1，x2是上述方程的两个实根，所以x1+x2=2+
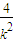，x1x2=1∵l1⊥l2，∴l2的斜率为
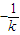
设D（x3，y3），E（x4，y4），则同理可得x3+x4=2+4k2，x3x4=1
∴|FA||FB|+|FD||FE|=（x1+1）（x2+1）+（x3+1）（x4+1）=8+4（k2+
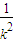）≥16（当且仅当k=±1时取等号）∴|FA|•|FB|+|FC|•|FD|的最小值为16．
点评：本题考查轨迹方程，考查直线与抛物线的位置关系，解题的关键是确定抛物线的方程，利用韦达定理解题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
轴的距离少1.
于
点，且
,
,
的值。