题目内容
对任意x∈R,给定区间[k-| 1 |
| 2 |
| 1 |
| 2 |
整数之差的绝对值.
(1)当x∈[-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)求f(
| 4 |
| 3 |
| 4 |
| 3 |
(3)当e-
| 1 |
| 2 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
分析:(1)当x∈[-
,
]时,根据定义,写出f(x)的解析式;当x∈[k-
,k+
](k∈z)时,由定义知:k为与x最近的一个整数,写出解析式即可;(2)根据(1)求得
f(
),f(-
)即可,利用奇偶性的定义即可判断函数f(x)(x∈R)的奇偶性,(3)要求方程f(x)-loga
=0的根,即求|x-k|-
logax=0的根,分类讨论,去掉绝对值符号,即可求得方程根的个数.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
f(
| 4 |
| 3 |
| 4 |
| 3 |
| x |
| 1 |
| 2 |
解答:解:(1)当x∈[-
,
]时,
由定义知:x与0距离最近,f(x)=|x|,x∈[-
,
]
当x∈[k-
,k+
](k∈z)时,
由定义知:k为与x最近的一个整数,故
f(x)=|x-k|,x∈[k-
,k+
](k∈z);
(2)f(
)=
,f(-
)=
判断f(x)是偶函数.
对任何x∈R,函数f(x)都存在,且存在k∈Z,满足
k-
≤x≤k+
,f(x)=|x-k|,
由k-
≤x≤k+
,可以得出-k-
≤-x≤-k+
,
即-x∈[-k-
,-k+
],
由(Ⅰ)的结论,f(-x)=|-x-(-k)|=|k-x|=|x-k|=f(x),
即f(x)是偶函数.
(3)解:f(x)-loga
=0,即|x-k|-
logax=0,
①当x>1时,|x-k|≥0>
logax,
∴|x-k|-
logax=0没有大于1的实根;
②容易验证x=1为方程|x-k|-
logax=0的实根;
③当
<x<1时,方程|x-k|-
logax=0变为1-x-
logax=0
设H(x)=
logax-(1-x)(
<x<1)
则H′(x)=
+1<
+1=-
+1<0,
所以当
<x<1时,H(x)为减函数,H(x)>H(1)=0,
所以方程没有
<x<1的实根;
④当0<x≤
时,方程|x-k|-
logax=0变为x-
logax=0
设G(x)=
logax-x(0<x≤
),显然G(x)为减函数,
∴G(x)≥G(
)=H(
)>0,
所以方程没有0<x≤
的实根.
综上可知,当e-
<a<1时,方程f(x)-loga
=0有且仅有一个实根,实根为1.
| 1 |
| 2 |
| 1 |
| 2 |
由定义知:x与0距离最近,f(x)=|x|,x∈[-
| 1 |
| 2 |
| 1 |
| 2 |
当x∈[k-
| 1 |
| 2 |
| 1 |
| 2 |
由定义知:k为与x最近的一个整数,故
f(x)=|x-k|,x∈[k-
| 1 |
| 2 |
| 1 |
| 2 |
(2)f(
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
判断f(x)是偶函数.
对任何x∈R,函数f(x)都存在,且存在k∈Z,满足
k-
| 1 |
| 2 |
| 1 |
| 2 |
由k-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即-x∈[-k-
| 1 |
| 2 |
| 1 |
| 2 |
由(Ⅰ)的结论,f(-x)=|-x-(-k)|=|k-x|=|x-k|=f(x),
即f(x)是偶函数.
(3)解:f(x)-loga
| x |
| 1 |
| 2 |
①当x>1时,|x-k|≥0>
| 1 |
| 2 |
∴|x-k|-
| 1 |
| 2 |
②容易验证x=1为方程|x-k|-
| 1 |
| 2 |
③当
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设H(x)=
| 1 |
| 2 |
| 1 |
| 2 |
则H′(x)=
| 1 |
| 2xlna |
| 1 | ||
2xlne-
|
| 1 |
| x |
所以当
| 1 |
| 2 |
所以方程没有
| 1 |
| 2 |
④当0<x≤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设G(x)=
| 1 |
| 2 |
| 1 |
| 2 |
∴G(x)≥G(
| 1 |
| 2 |
| 1 |
| 2 |
所以方程没有0<x≤
| 1 |
| 2 |
综上可知,当e-
| 1 |
| 2 |
| x |
点评:此题是中档题.考查新定义求函数的解析式,以及利用函数奇偶性的定义判断函数的奇偶性,分类讨论求方程根的个数问题,体现了分类讨论的思想,同时考查了利用应用知识分析解决问题的能力和运算能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 ,k+
,k+ ](k∈z),设函数f(x)表示实数x与x的给定区间内
](k∈z),设函数f(x)表示实数x与x的给定区间内 时,求出f(x)的解析式;当x∈[k-
时,求出f(x)的解析式;当x∈[k- ,k+
,k+ ](k∈z)时,写出用绝对值符号表示的f(x)的解析式;
](k∈z)时,写出用绝对值符号表示的f(x)的解析式;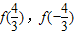 的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;
的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;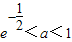 时,求方程
时,求方程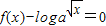 的实根.(要求说明理由
的实根.(要求说明理由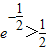 )
) ,k+
,k+ ](k∈z),设函数f(x)表示实数x与x的给定区间内
](k∈z),设函数f(x)表示实数x与x的给定区间内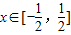 时,求出f(x)的解析式;当x∈[k-
时,求出f(x)的解析式;当x∈[k- ,k+
,k+ ](k∈z)时,写出用绝对值符号表示的f(x)的解析式;
](k∈z)时,写出用绝对值符号表示的f(x)的解析式;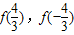 的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;
的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;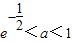 时,求方程
时,求方程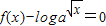 的实根.(要求说明理由
的实根.(要求说明理由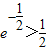 )
) ,k+
,k+ ](k∈z),设函数f(x)表示实数x与x的给定区间内
](k∈z),设函数f(x)表示实数x与x的给定区间内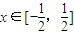 时,求出f(x)的解析式;当x∈[k-
时,求出f(x)的解析式;当x∈[k- ,k+
,k+ ](k∈z)时,写出用绝对值符号表示的f(x)的解析式;
](k∈z)时,写出用绝对值符号表示的f(x)的解析式;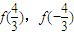 的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;
的值,判断函数f(x)(x∈R)的奇偶性,并证明你的结论;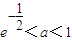 时,求方程
时,求方程 的实根.(要求说明理由
的实根.(要求说明理由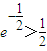 )
)