题目内容
对a、b∈R,记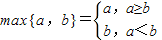 ,设f1(x)=|x-1|,
,设f1(x)=|x-1|, ,函数g(x)=max{f1(x),f2(x)},若方程g(x)=a有四个不同的实数解,则实数a的取值范围是 .
,函数g(x)=max{f1(x),f2(x)},若方程g(x)=a有四个不同的实数解,则实数a的取值范围是 .
【答案】分析:由题意可得当|x-1|≥-x2+6x-5时,g(x)=|x-1|,当|x-1|<-x2+6x-5时,g(x)=-x2+6x-5,据此可作出函数g(x)和y=a的图象,数形结合可得结论.
解答:解:由题意可知当|x-1|≥-x2+6x-5时,g(x)=|x-1|,
当|x-1|<-x2+6x-5时,g(x)=-x2+6x-5,
作出函数g(x)和y=a的图象如下:
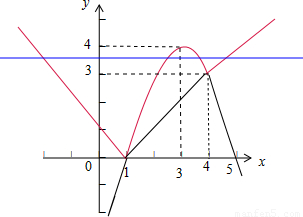
其中红色线为g(x)的图象,由图可知当a∈(3,4)时,
直线y=a和函数g(x)有4个不同的公共点,
故方程g(x)=a有四个不同的实数解,
故答案为:a∈(3,4)
点评:本题考查根的存在性和个数的判断,数形结合是解决问题的关键,属中档题.
解答:解:由题意可知当|x-1|≥-x2+6x-5时,g(x)=|x-1|,
当|x-1|<-x2+6x-5时,g(x)=-x2+6x-5,
作出函数g(x)和y=a的图象如下:

其中红色线为g(x)的图象,由图可知当a∈(3,4)时,
直线y=a和函数g(x)有4个不同的公共点,
故方程g(x)=a有四个不同的实数解,
故答案为:a∈(3,4)
点评:本题考查根的存在性和个数的判断,数形结合是解决问题的关键,属中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 .
.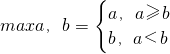 ,设f1(x)=|x-1|,
,设f1(x)=|x-1|,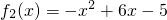 ,函数g(x)=max{f1(x),f2(x)},若方程g(x)=a有四个不同的实数解,则实数a的取值范围是________.
,函数g(x)=max{f1(x),f2(x)},若方程g(x)=a有四个不同的实数解,则实数a的取值范围是________.