题目内容
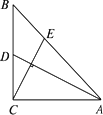
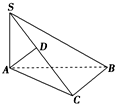
 已知△ABC中,C是以AB为直径圆上一点,SA⊥平面ABC,AD⊥SC.
已知△ABC中,C是以AB为直径圆上一点,SA⊥平面ABC,AD⊥SC.(Ⅰ)求证:AD⊥平面SBC;
(Ⅱ)已知SA=BC=3,AC=3
| 2 |
分析:(Ⅰ)要证明AD⊥平面SBC,因为AD⊥SC,只需证明AD⊥BC,进而转化为证明BC⊥平面SAC即可;
(Ⅱ)由(Ⅰ)知△ABC、△SAB均为Rt△,且∠SAB=∠ACB=90°,取SB中点M,易知M点即为三棱锥S-ABC外接球的球心,SB为外接球的直径,通过解直角三角形即可求得;
(Ⅱ)由(Ⅰ)知△ABC、△SAB均为Rt△,且∠SAB=∠ACB=90°,取SB中点M,易知M点即为三棱锥S-ABC外接球的球心,SB为外接球的直径,通过解直角三角形即可求得;
解答:(Ⅰ)证明:∵C是以为AB直径圆上一点,∴∠ACB=90°,∴BC⊥AC.
又SA⊥平面ABC,BC在平面ABC内,∴SA⊥BC.
又SA∩AC=A,∴BC⊥平面SAC,
又AD在平面SAC上,∴BC⊥AD.
又SC⊥AD,SC∩BC=C,∴AD⊥平面SBC.
(Ⅱ)解:由(Ⅰ)知△ABC、△SAB均为Rt△,且∠SAB=∠ACB=90°.
取SB中点M,连接AM、CM,则AM=CM=
SB.
所以SB为三棱锥S-ABC外接球直径;
又SA=BC=3,AC=3
所以AB2=AC2+BC2=27,SB2=SA2+AB2=36.
三棱锥S-ABC外接球半径为
SB=3.
故三棱锥S-ABC外接球体积V球=
×π×33=36π.
又SA⊥平面ABC,BC在平面ABC内,∴SA⊥BC.
又SA∩AC=A,∴BC⊥平面SAC,
又AD在平面SAC上,∴BC⊥AD.
又SC⊥AD,SC∩BC=C,∴AD⊥平面SBC.
(Ⅱ)解:由(Ⅰ)知△ABC、△SAB均为Rt△,且∠SAB=∠ACB=90°.
取SB中点M,连接AM、CM,则AM=CM=
| 1 |
| 2 |
所以SB为三棱锥S-ABC外接球直径;
又SA=BC=3,AC=3
| 2 |
所以AB2=AC2+BC2=27,SB2=SA2+AB2=36.
三棱锥S-ABC外接球半径为
| 1 |
| 2 |
故三棱锥S-ABC外接球体积V球=
| 4 |
| 3 |
点评:本题考查直线与平面垂直的判定、球的体积求解,考查学生的推理论证能力,属中档题.

练习册系列答案
相关题目
 已知△ABC中,C是以AB为直径圆上一点,SA⊥平面ABC,AD⊥SC.
已知△ABC中,C是以AB为直径圆上一点,SA⊥平面ABC,AD⊥SC.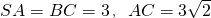 ,求三棱锥S-ABC外接球体积V球.
,求三棱锥S-ABC外接球体积V球.