题目内容
已知下列命题中真命题的个数是( )(1)若k∈R,且
 ,则k=0或
,则k=0或 ,
,(2)若
 ,则
,则 或
或 ,
,(3)若不平行的两个非零向量
 ,满足
,满足 ,则
,则 ,
,(4)若
 与
与 平行,则
平行,则 .
.A.0
B.1
C.2
D.3
【答案】分析:①由于数乘向量的结果也是零向量,则实数是零或向量是零向量;
②两向量的数量积为零,则两向量垂直或至少有一个为零向量;
③对于两非零向量,若有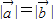 ,则
,则 即
即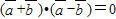 ;
;
④由于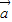 与
与 平行,则
平行,则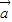 与
与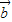 的方向相同或相反,故
的方向相同或相反,故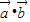 =±
=±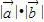 .
.
解答:解:①由于数乘向量的结果也是零向量,则实数是零或向量是零向量,
所以若k∈R,且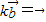 ,则k=0或
,则k=0或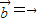 ,故①正确;
,故①正确;
②两向量的数量积为零,则两向量垂直或至少有一个为零向量,
所以“若 ,则
,则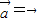 或
或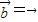 ”不正确,故②不正确;
”不正确,故②不正确;
③对于两非零向量,若有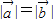 ,
,
则 即
即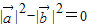 ,
,
所以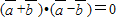 ,故③正确;
,故③正确;
④由于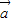 与
与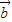 平行,则
平行,则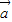 与
与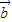 的方向相同或相反,
的方向相同或相反,
当方向相同时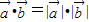 ,当方向不相同时
,当方向不相同时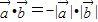 ,故④不正确.
,故④不正确.
故答案选C.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了向量的加、减、数乘运算数量积的运算及其几何意义,我们要根据已有的知识对四个结论逐一进行判断,可以得到正确的结论.
②两向量的数量积为零,则两向量垂直或至少有一个为零向量;
③对于两非零向量,若有
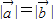 ,则
,则 即
即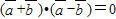 ;
;④由于
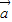 与
与 平行,则
平行,则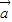 与
与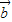 的方向相同或相反,故
的方向相同或相反,故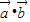 =±
=±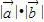 .
.解答:解:①由于数乘向量的结果也是零向量,则实数是零或向量是零向量,
所以若k∈R,且
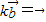 ,则k=0或
,则k=0或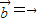 ,故①正确;
,故①正确;②两向量的数量积为零,则两向量垂直或至少有一个为零向量,
所以“若
 ,则
,则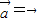 或
或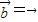 ”不正确,故②不正确;
”不正确,故②不正确;③对于两非零向量,若有
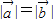 ,
,则
 即
即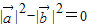 ,
,所以
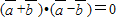 ,故③正确;
,故③正确;④由于
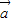 与
与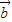 平行,则
平行,则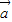 与
与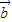 的方向相同或相反,
的方向相同或相反,当方向相同时
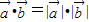 ,当方向不相同时
,当方向不相同时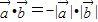 ,故④不正确.
,故④不正确.故答案选C.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了向量的加、减、数乘运算数量积的运算及其几何意义,我们要根据已有的知识对四个结论逐一进行判断,可以得到正确的结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,且
,且 ,则
,则 或
或 ,
, ,则
,则 或
或 ,满足
,满足 ,则
,则 ,
, 与
与 平行,则
平行,则 .
. B.
B. C.
C. D.
D.
 ,则k=0或
,则k=0或 ,
, ,则
,则 或
或 ,
, ,满足
,满足 ,则
,则 ,
, 与
与 平行,则
平行,则 .
.