题目内容
在复平面内,已知等边三角形的两个顶点所表示的复数分别为2,
+
i,求第三个顶点所表示的复数.
| 1 |
| 2 |
| ||
| 2 |
设第三个顶点所表示的复数为z那么根据题意,z-2和z-(
+
i)的模相等,辐角差为
(或-
),因而z-2=[z-(
+
i)](cos
+isin
)=(
+
i)z-(
+
i)2
[1-(
+
i)]z=2-[
+2•
•
i+(
i)2]
(
-
i)z=2-(-
+
i)∴z=2+
i;
或z-2=[z-(
+
i)](
-
i)=(
-
i)z-(
+
i)(
-
i),
(
+
i)z=2-(
+
),∴z=
-
i
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
[1-(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
或z-2=[z-(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |

练习册系列答案
相关题目
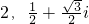 ,求第三个顶点所表示的复数.
,求第三个顶点所表示的复数.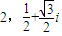 ,求第三个顶点所表示的复数.
,求第三个顶点所表示的复数.