题目内容
若直角坐标平面内A、B两点满足条件:①点A、B都在f(x)的图象上;②点A、B关于原点对称,则对称点对(A,B)是函数的一个“姊妹点对”(点对(A,B)与(B,A)可看作同一个“姊妹点对”).已知函数 f(x)=
,则f(x)的“姊妹点对”有( )个.
|
分析:首先弄清关于原点对称的点的特点,进而把问题转化为求方程
=-(x2+2x)的根的个数,再转化为求函数φ(x)=2ex+x2+2x零点的个数即可.
| 2 |
| e-x |
解答:解:设P(x,y) (x<0),则点P关于原点的对称点为P′(-x,-y),
于是
=-(x2+2x),化为2ex+x2+2x=0,
令φ(x)=2ex+x2+2x,下面证明方程φ(x)=0有两解.
由x2+2x≤0,解得-2≤x≤0,而
>0(x≥0),∴只要考虑x∈[-2,0]即可.
求导φ′(x)=2ex+2x+2,
令g(x)=2ex+2x+2,则g′(x)=2ex+2>0,
∴φ′(x)在区间[-2,0]上单调递增,
而φ′(-2)=2e-2-4+2<0,φ′(-1)=2e-1>0,
∴φ(x)在区间(-2,0)上只存在一个极值点x0.
而φ(-2)=2e-2>0,φ(-1)=2e-1-1<0,φ(0)=2>0,
∴函数φ(x)在区间(-2,-1),(-1,0)分别各有一个零点.
也就是说f(x)的“姊妹点对”有两个.
故选B.
于是
| 2 |
| e-x |
令φ(x)=2ex+x2+2x,下面证明方程φ(x)=0有两解.
由x2+2x≤0,解得-2≤x≤0,而
| 2 |
| ex |
求导φ′(x)=2ex+2x+2,
令g(x)=2ex+2x+2,则g′(x)=2ex+2>0,
∴φ′(x)在区间[-2,0]上单调递增,
而φ′(-2)=2e-2-4+2<0,φ′(-1)=2e-1>0,
∴φ(x)在区间(-2,0)上只存在一个极值点x0.
而φ(-2)=2e-2>0,φ(-1)=2e-1-1<0,φ(0)=2>0,
∴函数φ(x)在区间(-2,-1),(-1,0)分别各有一个零点.
也就是说f(x)的“姊妹点对”有两个.
故选B.
点评:本题考查了函数的零点,善于转化及熟练利用导数判断方程的根的个数是解决问题的关键.

练习册系列答案
相关题目
 的图象上;②点A、B关于原点对称,则点(A,B)是函数
的图象上;②点A、B关于原点对称,则点(A,B)是函数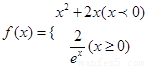 ,则
,则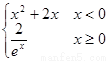 ,则f(x)的“姊妹点对”有 个。
,则f(x)的“姊妹点对”有 个。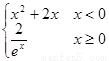 ,则f(x)的“姊妹点对”有
个
,则f(x)的“姊妹点对”有
个