题目内容
已知复数![]() 均为实数,
均为实数,![]() 为虚数单位,且对于任意复数
为虚数单位,且对于任意复数![]() 。
。
(Ⅰ)试求![]() 的值,并分别写出
的值,并分别写出![]() 和
和![]() 用
用![]() 、
、![]() 表示的关系式;
表示的关系式;
(Ⅱ)将(![]() 、
、![]() )作为点
)作为点![]() 的坐标,(
的坐标,(![]() 、
、![]() )作为点
)作为点![]() 的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点
的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点![]() 变到这一平面上的点
变到这一平面上的点![]() ,当点
,当点![]() 在直线
在直线![]() 上移动时,试求点
上移动时,试求点![]() 经该变换后得到的点
经该变换后得到的点![]() 的轨迹方程;
的轨迹方程;
(Ⅲ)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在该直线上?若存在,试求出所有这些直线;若不存在,则说明理由。
[解](1)由题设,![]() ,
,
于是由![]() ,
,
因此由![]() ,
,
得关系式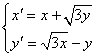
[解](2)设点![]() 在直线
在直线![]() 上,则其经变换后的点
上,则其经变换后的点![]() 满足
满足
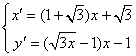 ,
,
消去![]() ,得
,得![]() ,
,
故点![]() 的轨迹方程为
的轨迹方程为![]()
[解](3)假设存在这样的直线,∵平行坐标轴的直线显然不满足条件,
∴所求直线可设为![]() ,
,
[解法一]∵该直线上的任一点![]() ,其经变换后得到的点
,其经变换后得到的点
![]() 仍在该直线上,
仍在该直线上,
∴![]() ,
,
即![]() ,
,
当![]() 时,方程组
时,方程组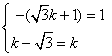 无解,
无解,
故这样的直线不存在。
当![]() 时,由
时,由![]()
得![]() ,
,
解得![]() 或
或![]() ,
,
故这样的直线存在,其方程为![]() 或
或![]() ,
,
[解法二]取直线上一点![]() ,其经变换后的点
,其经变换后的点![]() 仍在该直线上,
仍在该直线上,
∴![]() ,
,
得![]() , …(14分)
, …(14分)
故所求直线为![]() ,取直线上一点
,取直线上一点![]() ,其经变换后得到的点
,其经变换后得到的点![]() 仍在该直线上。
仍在该直线上。
∴![]() ,
,
即![]() ,得
,得![]() 或
或![]() ,
,
故这样的直线存在,其方程为![]() 或
或![]()

 阅读快车系列答案
阅读快车系列答案