题目内容
(1)若记数列{an}的前n项之和为Sn,试证明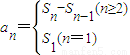 ;
;(2)已知数列{an}的前n项之和为Sn=2n2-n,求数列{an}的通项公式.
【答案】分析:(1)根据前n项和的定义有sn=a1+a2+a3+…+an-1+an,再由此产生sn-1=a1+a2+a3+…+an-1,两式作差即可.
(2)根据第一问的结论求解即可,一定要注意分类讨论.
解答:解:(1)①当n=1时,a1=s1
②当n≥2时,由数列的前n项和定义可得:
sn=a1+a2+a3+…+an-1+an(1)
sn-1=a1+a2+a3+…+an-1)(2)
∴(1)-(2)得:an=sn-sn-1
∴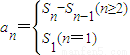
(2)由(1)知: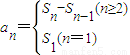
∴①当n=1时,a1=s1=1
②当n≥2时,an=sn-sn-1=2n2-n-(2(n-1)2-(n-1))=4n-3
综上:an=4n-3
点评:本题主要考查数列前n项和的定义及通项与前n项间的关系及其应用,做这类题,一定要注意分类讨论.
(2)根据第一问的结论求解即可,一定要注意分类讨论.
解答:解:(1)①当n=1时,a1=s1
②当n≥2时,由数列的前n项和定义可得:
sn=a1+a2+a3+…+an-1+an(1)
sn-1=a1+a2+a3+…+an-1)(2)
∴(1)-(2)得:an=sn-sn-1
∴
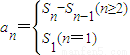
(2)由(1)知:
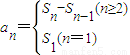
∴①当n=1时,a1=s1=1
②当n≥2时,an=sn-sn-1=2n2-n-(2(n-1)2-(n-1))=4n-3
综上:an=4n-3
点评:本题主要考查数列前n项和的定义及通项与前n项间的关系及其应用,做这类题,一定要注意分类讨论.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目