题目内容
如图,在四棱锥P-ABCD中,底面ABCD是正方形, 底面
底面 ,且PA=AB.
,且PA=AB.
(1)求证:BD 平面PAC;
平面PAC;
(2)求异面直线BC与PD所成的角.
(1)根据线面垂直的判定定理来得到 ,以及
,以及 是解决的核心。
是解决的核心。
(2)45º.
解析试题分析:(1)
证明:∵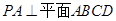 ,
, ,
, , 1分
, 1分
又 为正方形,
为正方形, , 2分
, 2分
而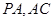 是平面
是平面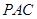 内的两条相交直线,
内的两条相交直线,  4分
4分
(2)解: ∵ 为正方形,
为正方形, ∥
∥ ,
,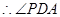 为异面直线
为异面直线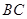 与
与 所成的角, 6分
所成的角, 6分
由已知可知,△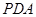 为直角三角形,又
为直角三角形,又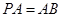 ,
,
∵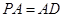 ,
, 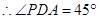 ,
,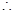 异面直线
异面直线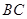 与
与 所成的角为45º. 8分
所成的角为45º. 8分
考点:异面直线所成的角,线面垂直
点评:主要是考查了空间中线面的垂直的证明,以及异面直线所成的角的求解,属于基础题。

练习册系列答案
相关题目

 的值.
的值.
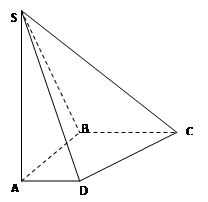

 中,
中,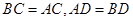 ,
,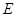 是
是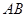 的中点.
的中点. 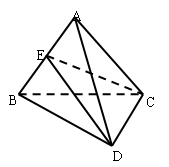
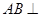 平面CDE;
平面CDE;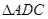 的重心,试在线段AE上确定一点F,使得GF//平面CDE.
的重心,试在线段AE上确定一点F,使得GF//平面CDE.
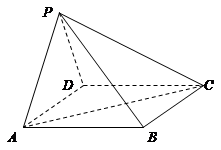
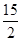 ,求AB的长.
,求AB的长.
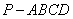 的底面
的底面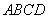 是等腰梯形,
是等腰梯形,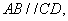 且
且
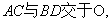

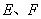 分别是
分别是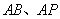 的中点.
的中点.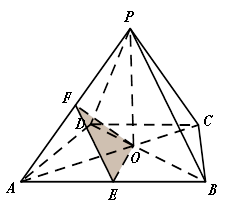
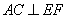 ;
;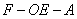 的余弦值.
的余弦值. 