题目内容
若实数a，b满足ab-4a-b+1=0 （a＞1），则（a+1）（b+2）的最小值为分析：先根据ab-4a-b+1=0求得a和b的关系式，进而代入到（a+1）（b+2）利用均值不等式求得答案．
解答：解：∵ab-4a-b+1═0
∴b=
=4+
∴（a+1）（b+2）=6a+
+3
=6a+
+9
=6（a-1）+
+15
≥27（当且仅当a-1=
即a=2时等号成立）
故答案为27．
∴b=
| 4a-1 |
| a-1 |
| 3 |
| a-1 |
∴（a+1）（b+2）=6a+
| 6a |
| a-1 |
=6a+
| 6 |
| a-1 |
=6（a-1）+
| 6 |
| a-1 |
≥27（当且仅当a-1=
| 1 |
| a-1 |
故答案为27．
点评：本题主要考查了基本不等式在最值问题中的应用．解题的关键是配出均值不等式的形式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在区间（0，1]上单调递减，在区间[1，+∞）上单调递增．若
，求函数f（x）的单调区间．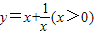
在区间（0，1]上单调递减，在区间[1，+∞）上单调递增．若
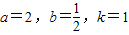，求函数f（x）的单调区间．